Multiple waves can be in the same position at the same time. Unlike particles, waves pass through each other without interacting.
When two waves are in the same position we say they are in superposition. The observed amplitude for waves in superposition is the sum of each wave's amplitude.
Ears are able to detect separate sound frequencies, even though they enter the ear in a superposition. This spectrogram lets you visualize the frequencies that make up various sounds.
The Wedge is a famous surf spot that has some dangerously fun waves because of interference from waves reflected off a jetty.
What is the amplitude of the rope when a crest lines up with a crest?
What is the amplitude of the rope when a crest lines up with a trough?
answer
Two crests add constructively to make a larger amplitude.
$$ 0.3\, \mathrm{m} + 0.3\, \mathrm{m} = 0.6\, \mathrm{m}$$A crest and trough add destructively to cancel out.
$$ 0.3\, \mathrm{m} - 0.3\, \mathrm{m} = 0\, \mathrm{m}$$Waves add constructively when both wave amplitudes are positive or both are negative. This produces a higher observed amplitude. Constructive interference is how two speakers playing the same song are louder than just one.
Example: Draw the superposition of these waves. They have the same wavelength, so they only add constructively.
solution
Waves add destructively when one wave amplitude is positive and the other is negative. This produces a lower observed amplitude. Destructive interference is put to use in noise cancelling headphones.
Example: Draw the superposition of these waves. They have the same wavelength but they are out of phase with each other. They can only add destructively.
solution
Example: Draw the superposition of these waves.
solution
Adding many sine waves together can produce some interesting waveforms. These waves are starting to look like sawtooth and triangle, but they need more contributing sine waves.
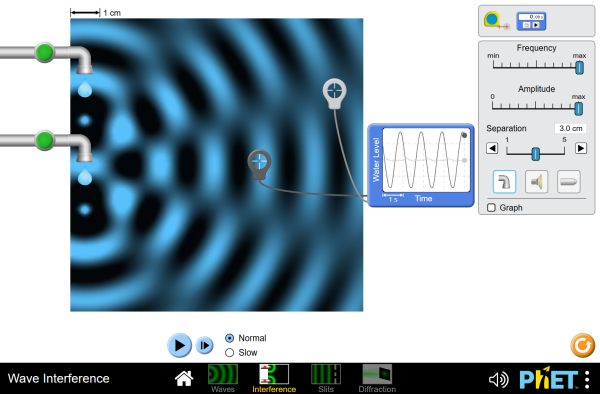
Interference is even more complex and interesting in higher dimensions.
Take a look at these 2-D ripple tank simulations:
Dipole
source: Two wave sources interfere.
Intersecting
Planes: Two wave planes interfere at 90°.
Beats:
Two wave sources with slightly different frequencies.
Consonance and Dissonance
Some of what makes music sound good depends on the cultural background of the listener. Listeners used to the western music tradition generally prefer sound waves that have a simple ratio between wavelengths.
solution
The first pair of frequencies has a harmonious 1:2 ratio.
I don't hate the second combination, but it does have a slight sour, tense, or sad sound to me. Of course, good music might find a place for that feeling.
Example: Draw the superposition of these waves. When waves have similar frequencies they produce a pattern called beats.
solution
You can decide if you hate the beats sound by clicking
frequency =volume =
frequency =
volume =
analyser =
The pattern in the graph above is sent as an electrical wave into your speakers. In the speaker, magnets convert the electrical wave into vibrations. The vibrations spread through the air as an audible wave of pressure.
For example, the major scale is a collection of notes that can sound nice together partly because they have a simple ratio between frequencies. Minor chords are collections of notes that might feel sad or tense partly because of the ratio between frequencies.
Diffraction
Waves tend to spread out in every direction possible within their medium. Diffraction is when a wave spreads out after some of the wave hits a barrier. This explains how sound can be heard through an open door even when there is no line of sight.
Diffraction can be explained by thinking of every point on a wavefront as the source of spherical waves. These spherical waves interfere with each other to produce different patterns.
You can see examples of diffraction in these 2-D ripple tank simulations:
Single Slit: Waves spread out in a circle as they pass through a gap.
Double Slit: Notice the pattern of constructive and destructive interference.
Half Plane: Waves curve around a wall.
Obstacle: Waves of the right wavelength can almost ignore a small barrier.
| Click to Run |
solution
solution
This is the famous quantum mechanical double slit experiment.
Notice the alternating constructive and destructive interference pattern.
The Doppler Effect
The Doppler effect is heard when a source of sound moves past an observer as a "vvvVVVRRROOOMMMmmm". The observed sound drops in frequency very quickly as the source zooms past.