Magnetism

Magnetic fields are a modification to electric fields that comes from special relativity. Like electric fields, magnetic fields are produced by charged particles, but only when the charged particle is moving.

Moving charges produce magnetic fields.

B v

A moving charge produces a magnetic field, but a moving charge also experiences a force from external magnetic fields.

Magnetic fields apply a force on moving charges.

For example, a moving electron produces a magnetic field. This field applies a force on other moving electrons.

Strong magnetic forces are produced through electromagnetism and ferromagnetism. Weaker forms of magnetism also exist, like diamagnetism and paramagnetism.

Magnetic Force on a Particle

The magnetic field in the diagram is directed out of the page. This field produces a force on moving charges. The direction of the magnetic force is inverted for negative charges.

v F v F

$$ F=qvB \sin \theta $$

\(F\) = magnetic force [N, newton, kg m/s²] vector
\(q\) = charge [C, Coulomb]
\(v\) = velocity [m/s] vector
\(B\) = external magnetic field [T, tesla, kg/C/s] vector
\(\theta\) = angle between v and B

What does ⨂ and ⊙ mean?
⨂ = into the page
⊙ = out of the page

To show 3D vectors we will use these symbols for into and out of the page. I think of the cross as the feathers on the back of an arrow, and the dot as the tip of an arrow.

Magnetic fields are measured in teslas, which can have a wide range of values.

Example: A +2 C particle is moving at 10 m/s through a 5 mT field from a refrigerator magnet. The velocity and field are at a right angle to each other. What magnitude force will be applied to the particle?
solution $$ F=qvB $$ $$ F = (2)(10)(0.005) $$ $$ F = 0.1 \, \mathrm{N} $$
Example: To measure the strength of a magnetic field, electrons are fired into the field at 100 m/s. The magnetic field accelerates the electrons at 255 m/s². What is the magnitude of the magnetic field perpendicular to the particle's velocity?
solution $$ F = ma $$ $$ F = (9.1 \times 10^{-31})(255)$$ $$ F = 2.32 \times 10^{-28} \, \mathrm{N}$$
$$ F = q v B $$ $$ B = \frac{F}{qv} $$ $$ B = \frac{2.32 \times 10^{-28}}{(1.6 \times 10^{-19})(100)} $$ $$ B = 1.45 \times 10^{-11} \, \mathrm{T} $$

Direction of Magnetic Forces

The 3D nature of the magnetic force can be solved with a vector operation called a cross product. The direction of a cross product can be found with the right hand rule.

v or I B F

Using your right hand, place your thumb in the direction of the current/charge. Place your index finger in the direction of the magnetic field. The palm of your hand will face in the direction of the force.

B v Example: What direction is the magnetic force on the charged particle?
solution

Using the right hand rule place your thumb towards the top of the page and your fingers to the right.

$$\text{into the page}$$
Example: A magnetic field is pointed north. A positively charged particle in the field is moving down, towards the ground. What direction is the magnetic force on the particle?
solution

Using the right hand rule place your thumb down and your index finger north.

$$\text{east}$$
Example: What direction magnetic field would produce a downward force on a negatively charged particle moving west?
solution

A negatively charged particle will go in the opposite direction of a positively charged particle. Using the right hand rule place your thumb west east and the palm of your hand down.

$$\text{south}$$
Example: A 1.0 C charged particle is moving west at 10 m/s through a 2 T magnetic field directed east. What is the magnitude and direction of the force on the particle?
solution

Since the velocity and magnetic field are in opposite directions there is no force.

$$F=qvB \sin \theta $$ $$\sin 180 = 0$$ $$F=0$$
Example: Find the magnitude and direction of the force on a 24 μC charge moving down at 13 m/s through an 8.5 T magnetic field directed south.
solution $$ F = q v B $$ $$ F = (24 \times 10^{-6})(13)(8.5) $$ $$ F = 0.00265 \, \text{N west}$$

Cloud chambers are a simple method of detecting high energy charged particles. In order to detect the particles, the chamber is filled with a supersaturated vapor of water or alcohol. High speed particles disrupt the vapor and leave a trail.

As radiation passes through the chamber only charged particles are visible. This is because neutral particles don't disrupt the vapor. When a powerful magnetic field is applied to the cloud chamber the charged particles curve. The arc of their curve indicates charge and mass.

Magnetic Force on a Wire

Running electric current through a wire moves a huge number of charges. Each charge follows F=qvB, but we can treat them as a whole with the concept of electric current.

derivation of magnetic force on a wire

We can substitute the definition of electric current and velocity.

$$I = \frac{q}{\Delta t} \quad \quad v = \color{teal}\frac{\Delta x}{\Delta t}$$ $$q = \color{magenta}I \Delta t \quad \quad \quad \quad \quad \, \,$$
$$F=qvB$$ $$F= {\color{magenta}(I \Delta t)} {\color{teal}\left( \frac{\Delta x}{\Delta t} \right )} B$$ $$F= I \Delta x B$$

We will use l for length instead of Δx.

$$F= I l B$$

A wire in a magnetic field will experience a force when current runs through it.

I F ℓ

$$ F=IlB \sin \theta $$

\(F\) = magnetic force [N, newton, kg m/s²] vector
\(I\) = current [A, Amps]
\(l\) = length of wire in the magnetic field [m, meter] vector
\(B\) = magnetic field [T, tesla, kg/C/s] vector
\(\theta\) = angle between the magnetic field and the current

Note that current is in the opposite direction of the flow of electrons, since electrons are negative.

The magnetic force can be used to build a rail gun.

Example: A 15 cm wire has 20 mA flowing through it east to west. The wire is in a magnetic field of 10 T directed up. Describe the force on the wire.
right hand rule v or I B F
solution $$ F=IlB$$ $$ F = (0.02)(0.15)(10) $$ $$ F = 0.03 \, \text{N north}$$
B I Example: A magnetic field is pointed to the right. Electric current is flowing towards the top of the page. What direction is the magnetic force on the wire?
solution

Using the right hand rule place your thumb towards the top of the page and your fingers to the right.

$$\text{into the page}$$
Example: How long is a wire that has a force of 0.050 N caused by the 0.21 A current interacting with a 0.45 T magnetic field at a right angle?
solution $$ F=lIB $$ $$ l= \frac{F}{IB} $$ $$ l= \frac{0.050}{(0.21)(0.45)} $$ $$ l= 0.53 \, \mathrm{m} $$

Electromagnets

The electric current from a long wire forms a magnetic field in the shape of concentric circles around the wire. The field strength diminishes with distance at 1/r not 1/r². The field strength can be calculated with Ampere's law.

I
Electric current in a straight wire produces a magnetic field that wraps around the wire.

The right hand grip rule can be used to find the direction the field turns around a wire. Place your right hand's thumb in the direction of the current. Your finger will curl in the direction the field turns.

This is different from the right hand rule used to find the force on a wire in a magnetic field.

B I
? Example: Curl the fingers on your right hand with the magnetic field to determine the direction of the current.
What does ⨂ and ⊙ mean?
⨂ = into the page
⊙ = out of the page

To show 3D vectors we will use these symbols for into and out of the page. I think of the cross as the feathers on the back of an arrow, and the dot as the tip of an arrow.

solution

Your thumb should point down. The current is directed towards the bottom of the page.

I

Two wires are aligned parallel at a constant distance of 0.3 m from each other. Each wire has 2.0 A of electric current moving towards the top of the page.

I I Example: What direction is the magnetic field produced by the current in the left wire at the location of the right wire?
solution

The field produced by the left wire is into the page on the right wire.

I

Example: What about the direction of the field from the right wire on the left?
solution

The field produced by the right wire is out of the page on the left wire.

I

Example: Use each wire's magnetic field to determine the direction of the forces between the wires.
solution

Wires with current in the same direction are pulled towards each other. I I F

This effect is part of why lightning manifests in thin strands. As electric charge travels between clouds and the ground the charge is pinched together forming lightning.

A loop of current produces a magnetic field with a north and south pole, like a ferromagnet.

The magnetic field from one wire can be increased by wrapping the wire in many loops. The strength can be increased again by wrapping the wire around a ferromagnetic material, like a nail.

Electromagnets are used in most devices that produce motion from electricity: DC motors, stepper motors, servos, speakers, microphones, valves, ...

They are also used in generators, MRI machines, transformers, induction heating, magnetic levitation ...

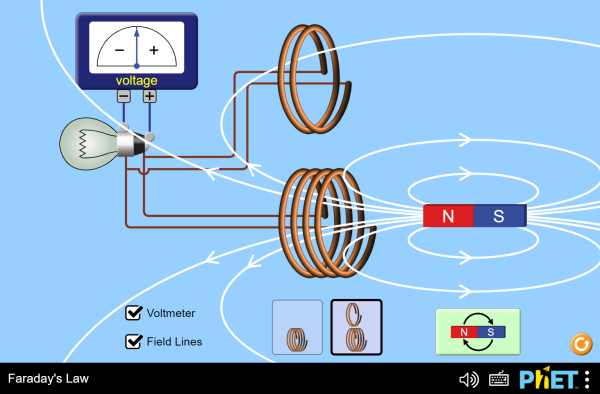
Electromagnetic induction is the production of electricity from wires moving through a magnetic field.

Induction is used to make electricity in most power generators.
Example: Nuclear, coal, hydroelectric, natural gas, and wind power

Faraday's Law
Click to Run

Ferromagnetism

Ferromagnetic metals produce a lasting magnetic field after they are exposed to an external magnetic field. Ferromagnetic metals include: iron, nickel, cobalt, most of their alloys, and rare earth metals.

Experiment: Test what materials ferromagnets are attracted to.
observations

Paper clips, staples, forks, screwdrivers, hammers, nails, scissors, refrigerators, cars, pans, speakers, microphones, batteries, phones.

Experiment: Put two ferromagnets near each other. What do you observe?
observations

One pair of ends attract and one pair repels.

A ferromagnet has a north and south pole just like an electromagnet. North and south poles attract, while two of the same poles repel.

If you break a magnet, each smaller piece also has a north and south pole. It's impossible to have a single north or south pole, a monopole.

You can see a 2D slice of the 3D field from a magnet by sprinkling small bits of iron around the magnet. The field has the same shape as the field from circular current in an electromagnet.

quantum explanation for the shape of ferromagnetic fields

Electrons do something similar to spinning around, but with some quantum mechanical differences. These electron "spins" count as moving charges, so they produce magnetic fields.

We don't see ferromagnetism in most materials because clockwise and counterclockwise electron spins cancel out. But in some materials the spins don't completely balance and we get ferromagnets.

Spinning electrons produce a magnetic field with the same shape as the field produced by electric current in a circular wire.

Magnetic field lines exit the north pole and enter the south pole. S N
Ferromagnets and electromagnets have a repulsive or attractive force that depends on which magnetic poles are facing each other.

  • Like poles repel               North+North, South+South
  • Opposite poles attract    North+South
    • derivation of the forces between north and south magnetic poles

    We learned in this example that current in parallel wires makes an attractive force and opposite current makes a repulsive force.

    Electromagnets and ferromagnets occur because they have charge moving in a circle, but it works the same way. Imagine two loops with parallel or opposite currents, and we can determine if the force between them is attractive or repulsive.

    If the current for each magnet is rotating in the same direction, the force between them is attractive. The top loop has a south pole facing down. The bottom loop has a north pole facing up.


    If the current for each magnets is rotating in opposite directions, the force between them is repulsive. Two north poles are facing each other.

    You can add multiple magnetic fields together to strengthen the total field.

    If you heat a magnet above it's curie temperature it loses it's property of ferromagnetism. The atomic-level magnetism become disordered due to increased thermal energy, and it no longer scales up to the macroscopic level.

    N S S N Question: What happens when you bring the north pole of a magnet close the north pole of another magnet?
    answer

    The magnets will repel each other.

    S N S N Question: What happens when you bring the south pole of a magnet close the north pole of another magnet?
    answer

    The magnets will attract each other.

    Question: What direction are the field lines at the north pole of a ferromagnet or an electromagnet?
    answer

    The north pole has field lines that are directed away from the magnet. The south pole has the same number of field lines directed into the magnet.

    I S N Question: What direction is the force the magnet is exerting on the wire?
    answer

    Using the right hand rule:

    the magnetic field is out of the north pole, to the right
    the electric current is up
    the force is into the page

    I S N Question: What direction is the force the magnet is exerting on the wire?
    answer

    Using the right hand rule:

    the magnetic field is out of the north pole, to the right
    the electric current is down
    the force is out of the page

    I S N Question: What direction is the force the magnet is exerting on the wire?
    answer

    This one is tricky. The field in the center of the wire is parallel with the current, so there is no force.

    The field at the left side of the magnet has a small component directed up. This produces a force on the left side of the wire directed out of the page. The field on the right side of the wire is into the page.

    These uneven forces on the sides of the wire will make it spin.

    I S N Question: What direction is the force the magnet is exerting on the wire?
    answer

    Using the right hand rule:

    the magnetic field is into the south pole, to the right
    the electric current is up
    the force is into the page

    Earth's Magnetic Field

    The Earth produces a magnetic field that is closely aligned with its axis of rotation. The source of the field is from convection of conductive materials in Earth's core, but the process is complex and has only been recently modeled with computer simulations.

    S N

    The Earth's magnetic field slows down charged particles. This shields the Earth from the solar wind's ionizing radiation. This slowing down can be seen at the north and south poles as an aurora.

    We have strong evidence that the north and south poles experience periodic reversals. About 780 000 years ago a compass would have pointed in the opposite direction it points now. The reversals are unpredictable, but typically there are thousands of years of stability between flips.

    0 10 20 30 40 50 60 70 80 90 350 340 330 320 310 300 290 280 270 180 170 160 150 140 130 120 110 100 190 200 210 220 230 240 250 260 N W E S NW SW NE SE N S

    A compass has a small magnet that aligns with the Earth's magnetic field.

    Question: The north pole of a magnet points towards the geographic north pole in the arctic circle. Does this make sense?
    answer

    This doesn't make sense. Two north poles would repel.

    The geographic north pole is actually the Earth's magnetic south pole.
    So confusing!

    Motion in a Magnetic Field

    The magnetic force on a charged particle in a uniform magnetic field is always at a 90 degree angle to the velocity. This satisfies the requirement for circular motion and it means we can set the equation for magnetic force equal to the centripetal force.

    derivation: the motion of a charged particle in a magnetic field $$ F = qvB \quad \quad F = \frac{mv^{2}}{r}$$ $$qvB = \frac{mv^{2}}{r}$$ $$qB = \frac{mv}{r}$$ $$r = \frac{mv}{qB}$$
    r v F

    $$r = \frac{mv}{qB}$$

    The Earth's magnetic field protects us from high speed charged particles. Most of these particles come from solar wind.

    Example: What is the radius for the circular motion of an electron in the Earth's magnetic field? Wikipedia says that the field is up to 70 μT, and particles from the solar wind travel at up to 500 km/s.
    solution $$r = \frac{mv}{qB}$$ $$r = \frac{(9.1 \times 10^{-31})(500\,000)}{(1.6 \times 10^{-19})(70 \times 10^{-6})}$$ $$r = 0.0406 \, \mathrm{m} $$
    Example: Find the radius for a proton in the same conditions.
    solution $$r = \frac{mv}{qB}$$ $$r = \frac{(1.67 \times 10^{-27})(500\,000)}{(1.6 \times 10^{-19})(70 \times 10^{-6})}$$ $$r = 74.55 \, \mathrm{m} $$

    Practice printout.pdf

    In case you wanted more practice I used AI to make some more problems. The rest of the site I made by hand, but generating endless problems seemed safe. I did find mistakes in the AI generated problems, and there are probably some I didn't find. Let me know if something could be fixed. I also added a practice problem on each page with no solution. That's intentional. Have fun!

    Use the right hand rule for a positive charge or conventional current, then reverse the force direction for a negative charge.

    Question: A positive particle moves north through a magnetic field pointed east in a lab diagram viewed from above. What direction is the magnetic force?
    answer

    Point your right thumb north and your fingers east. Your palm faces downward, so the force is down, toward the ground.

    Question: An electron moves north through a magnetic field pointed east. What direction is the magnetic force?
    answer

    A positive charge moving north in an eastward field would feel force downward. An electron is negative, so the force is reversed. The electron feels force upward.

    Question: A positive particle moves toward the top of the page through a magnetic field coming out of the page. What direction is the magnetic force?
    answer

    Point your thumb toward the top of the page and your fingers out of the page. Your palm faces right, so the force is to the right.

    Question: An electron moves to the right through a magnetic field directed into the page. What direction is the magnetic force?
    answer

    For a positive charge, thumb right and fingers into the page gives force toward the bottom of the page. An electron is negative, so the force is reversed toward the top of the page.

    Example: A +4.0 μC charge moves west at 1200 m/s through a 0.30 T magnetic field also directed west. What is the magnetic force magnitude?
    solution

    The velocity and magnetic field are parallel, so the angle is 0 degrees.

    $$F=qvB\sin\theta$$ $$F=(4.0\times10^{-6})(1200)(0.30)\sin(0^\circ)$$ $$F=0\,\mathrm{N}$$
    Example: A +3.0 μC particle moves at 2.0 km/s through a 40 mT magnetic field in a detector region. The velocity and field are perpendicular, and the detector is 12 cm wide. What magnetic force magnitude acts on it?
    solution $$q=3.0\times10^{-6}\,\mathrm{C}$$ $$v=2000\,\mathrm{m/s}$$ $$B=0.040\,\mathrm{T}$$ $$F=qvB\sin\theta$$ $$F=(3.0\times10^{-6})(2000)(0.040)\sin(90^\circ)$$ $$F=2.4\times10^{-4}\,\mathrm{N}$$
    Example: A +2.0 μC particle moves at 1500 m/s through a 0.25 T magnetic field. The velocity is 30 degrees from the field. What magnetic force magnitude acts on it?
    solution $$F=qvB\sin\theta$$ $$F=(2.0\times10^{-6})(1500)(0.25)\sin(30^\circ)$$ $$F=3.75\times10^{-4}\,\mathrm{N}$$
    Example: A particle with charge +4.0 μC moves perpendicular to a magnetic field at 3000 m/s and feels a 0.012 N magnetic force. What is the magnetic field strength?
    solution $$F=qvB$$ $$B=\frac{F}{qv}$$ $$B=\frac{0.012}{(4.0\times10^{-6})(3000)}$$ $$B=1.0\,\mathrm{T}$$
    Example: An electron moves perpendicular to a 30 mT magnetic field at 2.0 × 106 m/s. What is the electron's acceleration magnitude?
    solution

    Use magnetic force, then Newton's second law.

    $$B=0.030\,\mathrm{T}$$ $$F=qvB$$ $$F=(1.60\times10^{-19})(2.0\times10^6)(0.030)$$ $$F=9.6\times10^{-15}\,\mathrm{N}$$ $$a=\frac{F}{m}$$ $$a=\frac{9.6\times10^{-15}}{9.11\times10^{-31}}$$ $$a=1.1\times10^{16}\,\mathrm{m/s^2}$$
    Question: A charged particle moves through a magnetic field and curves in a circle at constant speed. Is the magnetic field doing work on the particle?
    answer

    No. The magnetic force is perpendicular to the velocity, so it changes the direction of motion but not the speed. The kinetic energy stays constant.

    Example: A straight wire carries 8.0 A through 15 cm of wire inside a 0.40 T magnetic field. The wire and field are perpendicular. What force acts on the wire?
    solution $$l=0.15\,\mathrm{m}$$ $$F=IlB\sin\theta$$ $$F=(8.0)(0.15)(0.40)\sin(90^\circ)$$ $$F=0.48\,\mathrm{N}$$
    Example: A 250 mA current flows through 8.0 cm of wire in a 0.60 T magnetic field. The wire and field are perpendicular. What magnetic force acts on the wire?
    solution $$I=0.250\,\mathrm{A}$$ $$l=0.080\,\mathrm{m}$$ $$F=IlB\sin\theta$$ $$F=(0.250)(0.080)(0.60)\sin(90^\circ)$$ $$F=0.012\,\mathrm{N}$$
    Example: A +3.0 μC particle moves at 1200 m/s through a 0.40 T magnetic field. What magnetic force acts on it?
    answer This cannot be solved from the information given. Magnetic force also needs the angle between the velocity and the magnetic field.
    Example: A wire carrying 3.0 A feels a 0.36 N force in a 0.20 T magnetic field. The wire and field are perpendicular. How much wire is inside the magnetic field?
    solution $$F=IlB$$ $$l=\frac{F}{IB}$$ $$l=\frac{0.36}{(3.0)(0.20)}$$ $$l=0.60\,\mathrm{m}$$
    Example: A 1.5 m wire carrying 12 A feels a 0.72 N force. The wire is perpendicular to the magnetic field. What is the field strength?
    solution $$F=IlB$$ $$B=\frac{F}{Il}$$ $$B=\frac{0.72}{(12)(1.5)}$$ $$B=0.040\,\mathrm{T}$$
    Question: A wire carries conventional current north through a magnetic field pointed upward. What direction is the force on the wire?
    answer

    Use the wire right hand rule: thumb north, fingers up. Your palm faces east, so the force is east.

    Question: A wire carries conventional current west through a magnetic field pointed downward. What direction is the force on the wire?
    answer

    Point your thumb west and your fingers downward. Your palm faces south, so the force is south.

    Example: Electrons drift south through a straight wire while the magnetic field points out of the page. What direction is the force on the wire?
    solution

    Conventional current points opposite electron drift, so the current is north. For a wire, use current direction: thumb north, fingers out of the page. Your palm faces east.

    $$\text{force on the wire: east}$$
    Question: A straight wire carries current out of the page in a flat page diagram. At a point higher on the page than the wire, what direction is the magnetic field from the wire?
    answer

    Use the right hand grip rule. Point your thumb out of the page. Your fingers curl counterclockwise, so at the top of the wire the magnetic field points left.

    Question: A vertical wire on the page carries current toward the top of the page. At a point to the right of the wire, what direction is the magnetic field from the wire?
    answer

    Use the right hand grip rule. Point your thumb toward the top of the page. On the right side of the wire, your fingers curl into the page.

    Question: Two long parallel wires carry current in the same direction. Do the wires attract or repel? What if the currents are opposite directions?
    answer

    Parallel currents in the same direction attract. Parallel currents in opposite directions repel.

    Example: An electron moves at 4.0 × 106 m/s perpendicular to a 20 mT magnetic field. What is the radius of its circular path?
    solution $$B=0.020\,\mathrm{T}$$ $$r=\frac{mv}{qB}$$ $$r=\frac{(9.11\times10^{-31})(4.0\times10^6)}{(1.60\times10^{-19})(0.020)}$$ $$r=1.14\times10^{-3}\,\mathrm{m}$$
    Example: A proton from the solar wind moves at 800 km/s perpendicular to a 50 μT part of Earth's magnetic field. What is the radius of its circular path?
    solution $$v=8.00\times10^5\,\mathrm{m/s}$$ $$B=50\times10^{-6}\,\mathrm{T}$$ $$r=\frac{mv}{qB}$$ $$r=\frac{(1.67\times10^{-27})(8.00\times10^5)}{(1.60\times10^{-19})(50\times10^{-6})}$$ $$r=167\,\mathrm{m}$$
    Example: A singly charged ion has mass 2.0 × 10-26 kg and moves at 6.0 × 105 m/s perpendicular to a 0.30 T magnetic field. What circular radius does it follow?
    solution

    Singly charged means the charge magnitude is one elementary charge.

    $$q=1.60\times10^{-19}\,\mathrm{C}$$ $$r=\frac{mv}{qB}$$ $$r=\frac{(2.0\times10^{-26})(6.0\times10^5)}{(1.60\times10^{-19})(0.30)}$$ $$r=0.25\,\mathrm{m}$$
    Example: An electron curves in a circular path with radius 4.0 cm inside a 0.50 T magnetic field. What speed does the electron have?
    solution $$r=\frac{mv}{qB}$$ $$v=\frac{rqB}{m}$$ $$v=\frac{(0.040)(1.60\times10^{-19})(0.50)}{9.11\times10^{-31}}$$ $$v=3.5\times10^9\,\mathrm{m/s}$$

    This is faster than light, so the classical equation is not physically reasonable here. The numbers describe a situation where relativity would be needed.

    Example: A proton starts from rest and is accelerated through a 2.0 kV potential difference. It then enters a 0.12 T magnetic field at a right angle inside a small vacuum chamber. What is the radius of its path?
    solution

    Use electric potential energy to find speed, then use the circular motion equation for a magnetic field.

    $$qV=\tfrac{1}{2}mv^2$$ $$v=\sqrt{\frac{2qV}{m}}$$ $$v=\sqrt{\frac{2(1.60\times10^{-19})(2000)}{1.67\times10^{-27}}}$$ $$v=6.2\times10^5\,\mathrm{m/s}$$ $$r=\frac{mv}{qB}$$ $$r=\frac{(1.67\times10^{-27})(6.2\times10^5)}{(1.60\times10^{-19})(0.12)}$$ $$r=0.054\,\mathrm{m}$$

    Reading (10 minutes): Read Auroras from NASA Science. Then answer these questions.

    According to the article, trace the energy transfer from the Sun to the visible light of an aurora.
    answer

    The solar wind carries energetic charged particles and magnetic fields away from the Sun. Their interaction with Earth's magnetosphere can deposit and store energy there. When that energy is released, energetic particles enter the upper atmosphere and collide with atoms and molecules. Those atoms and molecules release the transferred energy as visible light.


    Why do auroras usually appear near Earth's magnetic poles instead of equally across the planet?
    answer

    Earth's magnetic field guides many energetic charged particles along field lines toward the polar atmosphere. The particles are therefore more likely to enter the atmosphere and collide with gases near the poles, producing the northern and southern auroras.


    The Magnetism page says that magnetic force is perpendicular to a charged particle's velocity. How does that help explain the path of an auroral particle, and where does the energy that produces the glow come from?
    answer

    A perpendicular magnetic force changes the particle's direction and can guide it along a curved or spiraling path without directly increasing its speed. The energy that eventually produces the glow comes from the solar wind and energy stored in the magnetosphere. Atmospheric collisions transfer that energy to atoms and molecules, which then emit light.