Things fall. Pencils, buildings, people, everything falls.
The Earth is falling towards the Sun, but luckily it is falling in a way that doesn't hit the Sun.
An orbit.
Early Theories of Gravity
The history of gravity tells the story of humanity realizing we aren't the center of the universe.
The Greek philosopher Aristotle (384–322 BCE) believed that the natural place for the element of earth and water was down. The natural place for the elements of air and fire was up. He also believed that heavier objects fell faster than light objects.
Like many early philosophers, Aristotle organized the sky into a geocentric model. Moving planetary spheres surrounded a stationary and spherical Earth.
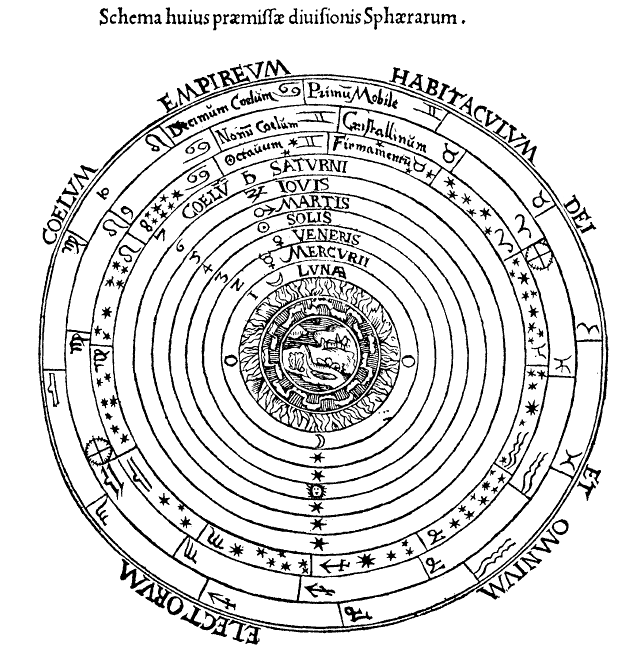
The geocentric models showed flaws. Planets would inexplicably change in speed and direction. To correct these flaws several small circles called epicycles were added to the path of the planets. As telescopes and data collection methods improved, the number of epicycles grew to correct for flaws in the geocentric model.
In 1543, Polish astronomer, Nicolaus Copernicus published a book on the heliocentric theory, the idea that the planets revolved around the Sun, not the Earth. His heliocentric theory marks the beginning of the scientific revolution.
Italian natural philosopher, Galileo Galilei, discovered that falling objects all accelerate at the same rate as long as air resistance isn't a significant factor.
Galileo also championed the heliocentric model even though it contradicted Catholic scripture. The leaders of the church asked him not to publish information that supported the heliocentric model, but Galileo continued. In response, the church forced him to recant his findings, they banned his work, and they sentenced him to house arrest from 1633 until his death in 1642.
solution
At the time it wasn't clear what model was the best one, but the heliocentric model explained the world in a more elegant and simple way. Issues like retrograde motion of planets was explained naturally in the heliocentric model without the need for epicycles.
One of the reasons Galileo liked the heliocentric model was that he had observed the Venus went through phases, just like the moon. In the Ptolemaic model, where Venus orbits the Earth, it wouldn't go through the full cycle of phases.
The heliocentric model was actually less accurate than the geocentric model. This is because the geocentric model was using a series of epicycles to improve on the circular paths both models used. Eventually, Kepler's Laws showed that with elliptical paths the heliocentric model was more accurate.
Kepler's Laws of Planetary Motion
In 1609, German astronomer, Johannes Kepler published 3 laws of planetary motion based on the heliocentric theory.
- The orbit of a planet is an ellipse with the Sun at one of the two foci. (F1, F2)
- A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. (A1 = A2)
- The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
$$ T^2 = r^3$$
\(T\) = orbital period, total time for one orbit [yr, years]
\(r\) = semi-major axis [AU, astronomical units, 1.5 × 1011 meters]
Kepler's laws mostly agreed with the Copernican model, but with a few improvements. In Kepler's model orbits moved in an ellipse, not a circle. The Sun wasn't the center of a planetary orbit, it was a foci of an elliptical orbit. Also, the planets would speed up and slow down as they orbited.
The semi-major axis of an ellipse is the distance from the center to the longest edge. For the Earth that distance is 149 597 870 700 m, which is called 1 astronomical unit (AU).
The orbital period squared equals the semi-major axis cubed for units of years (yr) and astronomical units (AU). The relationship is more complex with other units.modified equation for units of meters and seconds
$$T^2 = \frac{4 \pi^2}{GM} r^3$$\(T\) = orbital period, total time for one orbit [yr, years]
\(r\) = semi-major axis [AU, astronomical units, 1.5 × 1011 meters]
\(M\) = Mass of central body [kg, kilograms]
\(G\) = 6.67408 × 10-11 = universal gravitation constant [N m²/kg²]
solution
$$T^2 = r^3$$ $$T^2 = (1.524)^3$$ $$T^2 = 3.540$$ $$T = 1.88 \, \mathrm{yr}$$Each planet in the solar system lands somewhere on this graph. So this graph tells us that the farther a planet is from the sun, the longer it takes to orbit. A Jupiter year is much longer than an Earth year.
Universal Gravitation
In 1687 Isaac Newton published his book, Mathematical Principles of Natural Philosophy. The book contained his laws of motion and his law of universal gravitation. His reasoning was based on geometric proofs and his new mathematical techniques which are now called calculus.
Universal gravitation states that every particle in the universe is attracted to every other particle. It connects the heavens and the Earth with one equation. The same force that makes apples fall also controls the motion of stars, planets, and moons.
$$ F = \frac{GM_{1}M_{2}}{r^{2}} $$
\(F\) = force of gravity [N, newtons, kg m/s²]
vector
\(G\) = 6.67408 × 10-11 = universal gravitation constant [N m²/kg²]
\(M\) = mass [kg, kilograms]
\(r\) = distance between the center of each mass [m, meters]
Universal gravitation improved on Kepler's laws of planetary motion because it had a more universal application. Kepler's laws only applied to orbits where one body was much more massive, like the Sun and it's planets. Newton's gravitation applied to all matter.
No current theory perfectly describes reality. They all have the potential for improvement. In 1915 universal gravitation was improved on by Einstein's general relativity. It is hoped that one day we will improve on general relativity by combining it with quantum mechanics.
Each mass feels an equal but opposite force as predicted by Newton's 3rd law. This means that the same force of gravity you feel towards the Earth, the Earth feels towards you.
Question: Why don't we observe the Earth accelerating towards you?answer
The Earth and you both have the same force, but not the same acceleration.
$$F=ma$$ $$a = \frac{F}{m}$$Acceleration equals force divided by mass. The Earth has a large mass, so the acceleration from you pulling on the Earth is small.
Example: Find the force of gravity between the Earth and the Moon. The distance between them is 384 403 km.
solution
$$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24}) (7.346 \times 10^{22})}{(3.844 \times 10^{8})^{2}}$$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24}) (7.346 \times 10^{22})}{14.78 \times 10^{16}}$$ $$ F = \frac{6.674 \times 5.972 \times 7.346}{14.78} \times \frac{10^{-11}10^{24}10^{22}}{10^{16}}$$ $$ F = 19.798 \times 10^{19} \, \mathrm{N}$$solution
$$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24}) (2.00 \times 10^{30})}{(149.6 \times 10^{9})^{2}}$$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24}) (2.00 \times 10^{30})}{22380 \times 10^{18}}$$ $$ F = 3.561 \times 10^{22} \, \mathrm{N}$$solution
$$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24})(100)}{ 10\,000\,000^{2}}$$ $$ F = \frac{(6.674 \times 10^{-11})(5.972 \times 10^{24})(100)}{ 10^{14}}$$ $$ F = 398.57 \, \mathrm{N}$$solution
$$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ M_{1} = \frac{Fr^{2}}{GM_{2}}$$ $$ M_{1} = \frac{(100)(10\,000\,000)^{2}}{(6.674 \times 10^{-11})(5.972 \times 10^{24})}$$ $$ M_{1} = \frac{(100)(10^{14})}{(6.674 \times 10^{-11})(5.972 \times 10^{24})}$$ $$ M_{1} = 25.01 \, \mathrm{kg}$$solution
$$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ r^{2} = \frac{GM_{1}M_{2}}{F} $$ $$ r^{2} = \frac{(6.674 \times 10^{-11})(2.00 \times 10^{30})(2.2 \times 10^{14})}{3.65 \times 10^{12}} $$ $$ \sqrt{r^{2}} = \sqrt{8.04 \times 10^{21}} $$ $$ r = 8.97 \times 10^{10}\,\mathrm{m} $$solution
The force of gravity scales with distance and mass. The Earth is very close and very massive, so it's gravity is large enough to feel.
The force of gravity is very weak though. If gravity were stronger we might notice the pull from human sized objects.
Gravitational Acceleration
It is useful to adapt the universal gravitation equation to predict acceleration. To find acceleration we just need to divide an object's gravitational force by its mass.
derivation of universal gravitational acceleration
$$ F = mg $$ $$ \frac{F}{m} = g $$Newton's second law tells us we can replace F/M with acceleration.
$$ F = \frac{GM_{1}M_{2}}{r^{2}} $$ $$ \frac{F}{M_{2}} = \frac{GM_{1}}{r^{2}} $$ $$ g = \frac{GM_{1}}{r^{2}} $$$$ g = \frac{GM}{r^{2}} $$
\(g\) = acceleration of gravity [m/s²]
vector
\(G\) = \(\small 6.674 \times 10^{-11}\) = universal gravitation constant [m³/kg/s²]
\(M\) = mass of the body pulling [kg, kilograms]
(not the body experiencing the acceleration)
\(r\) = distance between the center of each mass [m, meters]
The acceleration vector is pointed towards the center of the mass producing the acceleration.
The mass of the body being accelerated isn't used in this equation. Use the mass of the body producing the acceleration. To find the acceleration of objects on Earth use Earth's mass.
The simulation below shows a vector field. Each vector shows the gravitational acceleration potentially felt at that location. These diagrams are helpful for predicting how a particle will accelerate.