Newton's Laws of Motion

Isaac Newton(1643-1727) made many profound contributions to science. He was an important figure in the Scientific Revolution. He worked on optics. He discovered universal gravitation. He also shares credit for inventing calculus.

In his work Philosophiæ Naturalis Principia Mathematica, Newton formulated his three laws of motion that model how objects accelerate. These laws make up the foundation of classical physics.

Hypothesis, Theory and Law

Science doesn't produce unchanging truths. Science is an ongoing process of discovery, and each new explanation has the potential to improve on the previous. Hypotheses, theories and laws could be true, but it is impossible to know anything with 100% certainty.


A phenomenon is an observable event, like the orbits of planets, static electricity, and lactose intolerance.

A hypothesis is a possible explanation for a phenomenon.

A scientific theory is a hypothesis that has been tested many times and never been proven false. Theories are explanations. They answer the question: why does this phenomenon occur? Examples include: quantum field theory, big bang theory, evolution, and germ theory.


A scientific law is also based on the results of many tests, but a law doesn't explain why a phenomenon occurs. Instead, laws are a general description of what has happened and what will happen for a narrow range of conditions.

  • Laws predict the behavior of a natural phenomenon.
  • Laws are only accurate for a limited range of conditions.
  • Laws are typically a mathematical equation, or a rule.

    • Almost all laws are found in the physical sciences. Some examples are: Ohm's Law, Universal Gravitation, Coulomb's law, and Kirchhoff's laws.





    Question: Why are scientific laws so rare in the life sciences?
    answer

    Most biological phenomenon are too complex to be explained by math.





    After observing the motion of the planets, Nicolaus Copernicus published the idea that the planets revolved around the sun. This idea was tested many times and never disproven. Sixty years later, Johannes Kepler discovered an equation that predicted how the planets moved around the sun.

    Question: Identify a phenomenon, hypothesis, theory, and law from the paragraph above.
    answer

    phenomenon: the motion of the planets
    hypothesis: planets revolve around the sun
    theory: planets revolve around the sun
    law: Kepler's equation





    Question: What about a scientific model? What does that word mean?
    answer

    A scientific model is a simplified representation of an aspect of reality. Models help us learn new things, predict how a complex system behaves, or guide future research. Models in physics often take the form of an equation, but they can also be a set of rules, or a physical thing.

    Generally, it is clear that a model doesn't match reality, but if the inaccuracy is small a model still has value.

  • the Ptolemaic model of the solar system
  • an infographic about the water cycle
  • a computer simulation
  • any physics equation

    • Newton's First Law: Inertia

    "A body either remains at rest or continues to move at a constant velocity, unless acted upon by a net external force."

    All matter has the property of Inertia. Matter stays still or keeps moving until a force causes it to accelerate.

    Most people already have a strong intuitive understanding of inertia. You probably know it's difficult to move something very heavy and easy to move something light. That's inertia.

    The Earth has orbited the Sun for billions of years without coming to a stop. It's clear that objects in space follow Newton's first law.

    Question: Objects on Earth seem to not follow Newton's first law. What causes objects on Earth to always come to a stop?
    answer

    The force of friction slows things down. As air particles strike a fast moving object the object slows down and the air speeds up. This spreads out the movement, but the movement is still there.

    m

    Press E to simulate the mass. Then press WASD to apply forces to the mass. Imagine the screen is the floor and you are looking down on the mass as it slides around, like air hockey.

    Simulation: What causes the mass to stop when you aren't pressing a key?
    observation

    Objects only change velocity if there is a force. In this case friction applies a force in the direction opposite the mass's velocity.

    Newton's Second Law: Force

    "The vector sum of the external forces F on an object is equal to the mass m of that object multiplied by the acceleration vector of the object."

    Newton's second law defined a new term called force. A body accelerates in the direction of the sum of the forces applied to it. The mass of the body determines how much acceleration is felt.

    m F F F

    $$\sum F=ma$$

    \( F \) = force [N, Newtons, kg m/s²] vector
    a push or a pull

    \(m\) = mass [kg, kilogram]
    resistance to acceleration

    \(a\) = acceleration [m/s²] vector

    \( \sum \) = The greek letter Sigma represents a summation of numbers. It means add up all the forces to get a net force.

    $$\sum F=F_{1}+F_{2}+F_{3}+...$$

    If there was a 5 N force to the left and a 20 N force to the right we could get the net force by adding them. Force is a vector, so the left force should be negative.

    $$\sum F= - 5 \, \mathrm{N} + 20 \, \mathrm{N} $$ $$\sum F= 15 \, \mathrm{N}$$
    Example: A ball has a mass of 0.43 kg. Find the acceleration of the ball when it experiences a net force (total force) of 1 N from air friction.
    solution
    $$m = 0.43\,\mathrm{kg}$$ $$\sum F = 1\,\mathrm{N}$$ $$a = \, ?$$
    $$\sum F=ma$$ $$\frac{\sum F}{m}=a$$ $$\frac{1 \, \mathrm{N}}{0.43 \, \mathrm{kg}}=a$$ $$\frac{1 \, \mathrm{kg \frac{m}{s^2}}} {0.43 \, \mathrm{kg} }=a$$ $$2.33 \, \mathrm{\tfrac{m}{s^2}}=a$$
    100 kg 2000 N 1900 N Example: A 100 kg boat at rest is being pushed left with a 2000 N force from the wind. The water current is producing a force of 1900 N to the right. How will the boat accelerate? How far will the boat go in 6 s?
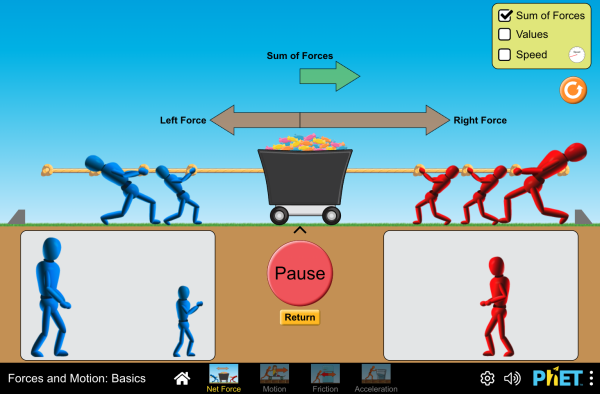
    solution $$ \text{Vectors pointed down or left are negative.}$$ $$\sum F=ma$$ $$-2000+1900=(100)(a)$$ $$-100=(100)(a)$$ $$-1 \mathrm{\tfrac{m}{s^{2}}}= a$$ $$ \text{The boat will accelerate to the left.}$$ $$ u = 0 $$ $$ \Delta x = ?$$ $$ \Delta t = 6\mathrm{s}$$ $$ \Delta x = u\Delta t+ \tfrac{1}{2} a \Delta t^{2}$$ $$ \Delta x = (0)(6)+\tfrac{1}{2} (-1)(6)^{2}$$ $$ \Delta x = \tfrac{1}{2} (-1)(6)^{2}$$ $$ \Delta x = -18 \, \mathrm{m}$$ $$ \text{The boat will move 18 meters to the left.}$$

    Play around with the net force simulation to get a feeling for how adding force vectors produces acceleration.

    Forces and Motion: Basics
    Click to Run

    Question: Could the tug of war be moving left, but have a net force to the right?
    answer

    An object could be moving in one direction and have a force in the opposite direction if it was slowing down.

    To test this out, add one person to the left. Click go. Wait a second. Add two on the right.


    Question: On the motion mode, find the mass of the gift.
    answer

    We need to solve a 1-D motion problem with constant accelerate. We can record the initial and final velocities if you check the "values" and "speed" boxes. Get a stopwatch to record the time elapsed.

    After we use a kinematics equation to solve for acceleration, we can use Newton's 2nd law to calculate the mass.

    solution

    I applied a 10N force for 10 seconds and recorded the time and velocities.

    $$u = 0 $$ $$v = 2 \, \mathrm{\tfrac{m}{s}}$$ $$\Delta t = 10 \, \mathrm{s}$$ $$a = \, ?$$
    $$v = u + a \Delta t$$ $$2 \, \mathrm{\tfrac{m}{s}} = 0 + a (10 \, \mathrm{s})$$ $$a = 0.2 \, \mathrm{\tfrac{m}{s^2} }$$
    $$\sum F=ma$$ $$10 \, \mathrm{N} = m (0.2 \, \mathrm{\tfrac{m}{s^2}})$$ $$\frac{10 \, \mathrm{N}}{0.2 \, \mathrm{\tfrac{m}{s^2}}} = m$$ $$50 \, \mathrm{kg} = m$$

    Question: If I apply a force to a mass it accelerates. What happens if I apply a larger force to the same mass?
    answer

    Mass is constant so we can just pretend it is one.

    $$F=ma$$ $$F=a$$ $${\Uparrow \atop F} {\atop =} {\Uparrow \atop a} $$

    Force and acceleration are directly proportional. Increasing F will cause a proportional increase in a.

    Question: If I apply a 100 N force to a mass it accelerates at 2 m/s². What happens if I double the mass while keeping the force the same?
    answer

    Force is constant so we can just pretend it is one.

    $$F=ma$$ $$1=ma$$ $$1=(2m)\left(\tfrac{1}{2} a \right)$$

    Mass and acceleration are inversely proportional. Doubling m will cause a to be halved.

    Newton's Third Law:
    Equal and Opposite Force Pairs

    "When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body."


    F 1 F 2 $$F_1 = -F_2$$

    If you push on something it will push back with the same force, but in the opposite direction. Forces always come in equal, but opposite pairs.

    Most of the time force pairs come from objects in contact, but even non-contact forces, like gravity, still obey this law.

    Question: You push down on the ground with a 1000 N force. Describe the magnitude and direction of the force the ground pushes on you.
    answer

    The force the ground applies is equal and opposite to the force you apply on the ground. The magnitude is 1000 N. The direction is up.

    Question: A boxer's glove applies a 140 N force to the face of another boxer. Describe the magnitude of the force the face applies to the glove.
    answer

    When a fist is punching a face, the face is also punching the fist. That's deep...

    Anyways, the force is equal and opposite. The magnitude is 140 N.

    Example: You (100 kg) are standing on a frictionless skateboard. You throw your 2 kg bottle of water to the right. During the throw, the water bottle briefly accelerates at 40 m/s². How much acceleration do you feel at that time?
    strategy

    Calculate the force the water bottle feels when it accelerates at 40 m/s². Plug the negative value of that force in as the force you feel.

    solution

    The force the water bottle feels is equal and opposite to the force you feel.

    $$ \text{water bottle}$$ $$F = ma $$ $$F=(2\, \mathrm{kg})(40\,\mathrm{\tfrac{m}{s^2}} )$$ $$F=\color{#80f}80 \, \mathrm{N}$$
    $$ \text{you}$$ $$F = ma $$ $$- {\color{#80f}80 \, \mathrm{N}} = (100 \, \mathrm{kg}) a$$ $$-0.8 \, \mathrm{\tfrac{m}{s^2}}=a$$