The calculations for fluid friction are beautiful, but difficult. Instead, we are going to focus on the two types of dry friction: static and kinetic. Dry friction occurs when two solid surfaces are in contact.
Even seemingly smooth surfaces are rough at the microscopic level. Dry friction can occur because rough surfaces get caught on each other. This causes microscopic deformations to occur. Friction can also come from other sources like chemical bonding between surfaces.
Dry friction is difficult to model because surfaces can have a wide range of shapes and chemical compositions. These 5 rules are broken as often as they are followed.
This friction model is only a "rough" approximation, so don't expect much precision or accuracy.
Static Friction
Static means not moving. Static friction is friction between solid objects that are not moving relative to each other. For example, static friction can prevent an object from sliding down a sloped surface.
The static friction force balances applied forces to keep the object stationary. We can estimate the maximum static friction force.
$$ F_s \leq \mu_{s} F_{N}$$
\(F_s\) = force of static friction [N, newtons]
direction and magnitude change to keep acceleration zero
but only up to the maximum value
\(F_N\) = normal force [N, newtons]
\(\mu_s\) = mu, coefficient of friction [no units]
Friction Coefficient Data Table (wikipedia)
| Materials | Static Friction | Kinetic Friction | |||
|---|---|---|---|---|---|
| Dry | Lubricated | Dry | Lubricated | ||
| Aluminium | Steel | 0.61 | 0.47 | ||
| Aluminum | Aluminum | 1.5 | |||
| Gold | Gold | 2.5 | |||
| Platinum | Platinum | 3.0 | |||
| Silver | Silver | 1.5 | |||
| Alumina ceramic | Silicon Nitride ceramic | 0.004 (wet) | |||
| BAM (Ceramic alloy AlMgB14) | Titanium boride (TiB2) | 0.04–0.05 | 0.02 | ||
| Brass | Steel | 0.35-0.51 | 0.19 | 0.44 | |
| Cast iron | Copper | 1.05 | 0.29 | ||
| Cast iron | Zinc | 0.85 | 0.21 | ||
| Concrete | Rubber | 1.0 | 0.30 (wet) | 0.6-0.85 | 0.45-0.75 (wet) |
| Concrete | Wood | 0.62 | |||
| Copper | Glass | 0.68 | |||
| Copper | Steel | 0.53 | 0.36 | ||
| Glass | Glass | 0.9-1.0 | 0.4 | ||
| Human synovial fluid | Cartilage | 0.01 | 0.003 | ||
| Ice | Ice | 0.02-0.09 | |||
| Polyethene | Steel | 0.2 | 0.2 | ||
| (Teflon) | PTFE (Teflon) | 0.04 | 0.04 | 0.04 | |
| Steel | Ice | 0.03 | |||
| Steel | PTFE (Teflon) | 0.04 | 0.04 | 0.04 | |
| Steel | Steel | 0.74 | 0.16 | 0.42-0.62 | |
| Wood | Metal | 0.2–0.6 | 0.2 (wet) | ||
| Wood | Wood | 0.25–0.5 | 0.2 (wet) | ||
solution
$$ F_s \leq \mu_{s} F_{N} $$ $$ F_{s\mathrm{\,max}} = \mu_{s} F_{N} $$ $$F_{N}=mg$$ $$F_{s\mathrm{\,max}}= \mu_{s}mg$$ $$F_{s\mathrm{\,max}}= (0.68)(0.42)(9.8)$$ $$F_{s\mathrm{\,max}}= 2.80 \, \mathrm{N}$$solution
Include both masses in the total mass.
$$F_g = mg$$ $$F_g = (20)(9.8)$$ $$F_g = 196\,\mathrm{N}$$ Since the block isn't accelerating in the vertical the normal force equals the force of gravity for both blocks. $$F_{s\mathrm{\,max}} = \mu_s F_N$$ $$F_{s\mathrm{\,max}} = \mu_s F_g$$ $$F_{s\mathrm{\,max}} = \mu_s 196$$ The coefficient of static friction for concrete and wood is 0.62. $$F_{s\mathrm{\,max}} = (0.62) (196)$$ $$F_{s\mathrm{\,max}} = 122 \, \mathrm{N}$$Example: Calculate the maximum value the hanging mass could have before the two masses begin to move. You can test your answer in the simulation.
The 5 kg block is made of aluminum and the table is made of steel.
Friction Coefficient Data Table (wikipedia)
| Materials | Static Friction | Kinetic Friction | |||
|---|---|---|---|---|---|
| Dry | Lubricated | Dry | Lubricated | ||
| Aluminium | Steel | 0.61 | 0.47 | ||
| Aluminum | Aluminum | 1.5 | |||
| Gold | Gold | 2.5 | |||
| Platinum | Platinum | 3.0 | |||
| Silver | Silver | 1.5 | |||
| Alumina ceramic | Silicon Nitride ceramic | 0.004 (wet) | |||
| BAM (Ceramic alloy AlMgB14) | Titanium boride (TiB2) | 0.04–0.05 | 0.02 | ||
| Brass | Steel | 0.35-0.51 | 0.19 | 0.44 | |
| Cast iron | Copper | 1.05 | 0.29 | ||
| Cast iron | Zinc | 0.85 | 0.21 | ||
| Concrete | Rubber | 1.0 | 0.30 (wet) | 0.6-0.85 | 0.45-0.75 (wet) |
| Concrete | Wood | 0.62 | |||
| Copper | Glass | 0.68 | |||
| Copper | Steel | 0.53 | 0.36 | ||
| Glass | Glass | 0.9-1.0 | 0.4 | ||
| Human synovial fluid | Cartilage | 0.01 | 0.003 | ||
| Ice | Ice | 0.02-0.09 | |||
| Polyethene | Steel | 0.2 | 0.2 | ||
| (Teflon) | PTFE (Teflon) | 0.04 | 0.04 | 0.04 | |
| Steel | Ice | 0.03 | |||
| Steel | PTFE (Teflon) | 0.04 | 0.04 | 0.04 | |
| Steel | Steel | 0.74 | 0.16 | 0.42-0.62 | |
| Wood | Metal | 0.2–0.6 | 0.2 (wet) | ||
| Wood | Wood | 0.25–0.5 | 0.2 (wet) | ||
hint
First, draw a free body diagram. Then calculate the max static friction force on the 5 kg block.
Since the blocks aren't moving, the opposing forces are equal. The friction force equals the tension force, which also equals the force of gravity for the right block. This means we can set the max static friction equal to the force of gravity for the right block.
Replace the force of gravity with "mg", and solve for the mass.
solution
Since the system isn't moving the acceleration is zero. This means that opposing forces need to be equal. The friction force equals the tension force, which also equals the force of gravity on the right block.
$$F_{s\mathrm{\,max}} = T = F_g = mg$$ $$F_{s\mathrm{\,max}} = mg$$ $$29.89 = m(9.8)$$ $$m = 3.05 \, \mathrm{kg}$$Kinetic Friction
Kinetic means motion. Kinetic friction is a force that occurs when two surfaces in contact slide against each other. The kinetic friction force remains constant over a wide range of speeds.
$$F_{k}=\mu_{k} F_{N}$$
\(F_k\) = force of kinetic friction [N,newtons]
pointed opposite the direction of motion
\(F_N\) = normal force [N,newtons]
\(\mu _k\) = mu, coefficient of friction [no units]
In most situations, the friction force doesn't depend on the amount of contact between surfaces. This is because a larger contact area spreads out the normal force.
Find the force of kinetic friction, and the time for the cup to come to a stop.
Friction Coefficient Data Table (wikipedia)
| Materials | Static Friction | Kinetic Friction | |||
|---|---|---|---|---|---|
| Dry | Lubricated | Dry | Lubricated | ||
| Aluminium | Steel | 0.61 | 0.47 | ||
| Aluminum | Aluminum | 1.5 | |||
| Gold | Gold | 2.5 | |||
| Platinum | Platinum | 3.0 | |||
| Silver | Silver | 1.5 | |||
| Alumina ceramic | Silicon Nitride ceramic | 0.004 (wet) | |||
| BAM (Ceramic alloy AlMgB14) | Titanium boride (TiB2) | 0.04–0.05 | 0.02 | ||
| Brass | Steel | 0.35-0.51 | 0.19 | 0.44 | |
| Cast iron | Copper | 1.05 | 0.29 | ||
| Cast iron | Zinc | 0.85 | 0.21 | ||
| Concrete | Rubber | 1.0 | 0.30 (wet) | 0.6-0.85 | 0.45-0.75 (wet) |
| Concrete | Wood | 0.62 | |||
| Copper | Glass | 0.68 | |||
| Copper | Steel | 0.53 | 0.36 | ||
| Glass | Glass | 0.9-1.0 | 0.4 | ||
| Human synovial fluid | Cartilage | 0.01 | 0.003 | ||
| Ice | Ice | 0.02-0.09 | |||
| Polyethene | Steel | 0.2 | 0.2 | ||
| (Teflon) | PTFE (Teflon) | 0.04 | 0.04 | 0.04 | |
| Steel | Ice | 0.03 | |||
| Steel | PTFE (Teflon) | 0.04 | 0.04 | 0.04 | |
| Steel | Steel | 0.74 | 0.16 | 0.42-0.62 | |
| Wood | Metal | 0.2–0.6 | 0.2 (wet) | ||
| Wood | Wood | 0.25–0.5 | 0.2 (wet) | ||
solution
$$F_{k}= \mu_{k}F_{N}$$ $$F_{N}=mg$$ $$F_{k}= \mu_{k}mg$$ $$F_{k}= (0.4)(0.42)(9.8)$$ $$F_{k}= 1.64 \, \mathrm{N}$$$$F=ma$$ $$\frac{F}{m}=a$$ $$\frac{1.64}{0.42}=a$$ $$3.90 \mathrm{\tfrac{m}{s^{2}}} = a$$
$$a=-3.90 \mathrm{\tfrac{m}{s^{2}}} \quad \Delta t=? \quad v_{i}=3.0 \mathrm{\tfrac{m}{s}}\quad v_{f}=0$$ $$v_{f} = v_{i}+a \Delta t$$ $$\frac{v_{f} - v_{i}}{a}=\Delta t$$ $$\frac{0 - 3}{-3.90}=\Delta t$$ $$0.77 \mathrm{s}=\Delta t$$
Static friction will match an applied force until the applied force exceeds the maximum value of static friction. Forces above that point will cause motion.
Once the body is moving, friction transitions to kinetic. Kinetic friction is lower and less precise. This transition often causes a jerky motion as the friction force quickly drops to the lower value.
Example: Imagine the graph above is for a 20 kg box. Calculate the coefficients of kinetic and static friction.kinetic friction solution
$$F_N = F_g = mg$$ $$F_N = (20 \, \mathrm{kg})(9.8 \, \mathrm{ \tfrac{m}{s^2}}) $$ $$F_N = 196 \, \mathrm{N}$$We can tell from the graph that the force of kinetic friction is about 70 N.
$$F_k = \mu_{k} F_{N} $$ $$70 \, \mathrm{N}= \mu_{k} 196 \, \mathrm{N}$$ $$\frac{70 \, \mathrm{N}}{196 \, \mathrm{N}} = \mu_{k} $$ $$0.36 = \mu_{k}$$static friction solution
$$F_N = F_g = mg$$ $$F_N = (20 \, \mathrm{kg})(9.8 \, \mathrm{ \tfrac{m}{s^2}}) $$ $$F_N = 196 \, \mathrm{N}$$We can tell from the dotted line that the max value of static friction is 100 N.
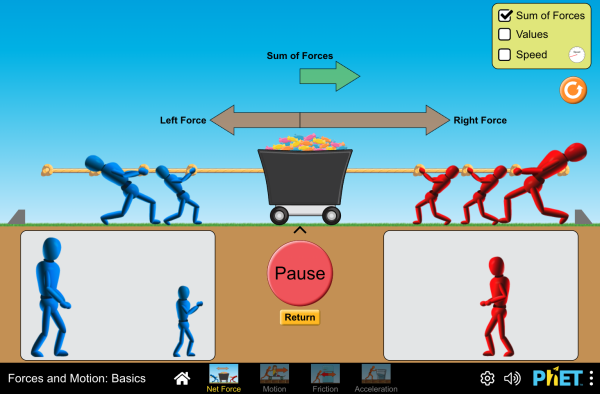
$$ F_s \leq \mu_{s} F_{N} $$ $$ F_{s\mathrm{\,max}} = \mu_{s} F_{N} $$ $$ 100 \, \mathrm{N} = \mu_{s} 196 \, \mathrm{N}$$ $$\frac{100 \, \mathrm{N}}{196 \, \mathrm{N}} = \mu_{s} $$ $$0.51 = \mu_{s}$$Simulation: Calculate the coefficients of kinetic and static friction? Use the default settings on the friction mode for the simulation above.
coefficient of static friction solution
Click the reset icon to make sure the simulation is at the default friction.
Check the "Masses" box.
Slowly increase the force until the mass moves.
This is the maximum force of static friction. I got 125 N. $$F_{\mathrm{max}}= \mu_{s}F_{N}$$
$$F_{\mathrm{max}}= \mu_{s}mg$$
$$\frac{F_{\mathrm{max}}}{mg} = \mu_{s}$$
$$\frac{125}{(50)(9.8)} = \mu_{s}$$ $$0.255 = \mu_{s}$$
coefficient of kinetic friction solution
Click the reset icon to make sure the simulation is at the default friction.
Check the "Forces" and "Values" boxes.
Set the applied force to be enough to keep the box moving.
You should be able to see the value of the friction force. (94 N)
What variables determine the coefficient of static friction?
solution
Gravity isn't in the same directions as the other forces so we can't use Newton's second law. We need to separate the gravity vector into components parallel and perpendicular to the ground.
$$F_{g}=mg$$-
$$\text{perpendicular to ground}$$
$$F_{g\perp}=F_{g}\cos(\theta)$$ $$F_{g\perp}=mg\cos(\theta)$$ -
$$\text{parallel to ground}$$
$$F_{g\parallel}=F_{g}\sin(\theta)$$ $$F_{g\parallel}=mg\sin(\theta)$$
Since the acceleration is zero all opposite forces must be the same.
This tells us the normal force and the static friction force.
$$F_N = F_{g\perp}=mg \cos{\theta}$$ $$F_s =F_{g\parallel}= mg \sin{\theta}$$For the maximum angle, right at the point where the mass will start to slide, we can use the static friction equation.
$$F_{\mathrm{s\,max}} = \mu_s F_N$$The maximum static friction will equal the parallel component of gravity at the largest possible angle before the mass will start to slide.
$$F_{g\parallel} = F_{\mathrm{s\,max}}$$ $$F_{g\parallel} = \mu_s F_N$$ $$mg \sin{\theta}= \mu_s mg \cos{\theta}$$ $$ \sin{\theta}= \mu_s \cos{\theta}$$ $$ \frac{\sin{\theta}}{\cos{\theta}}= \mu_s $$ $$ \boxed{\tan{\theta}= \mu_s} $$The angle at which an object begins to slide depends on only the coefficient of static friction, not the mass or the acceleration of gravity!
What variables determine the coefficient of kinetic friction?
solution
Gravity isn't in the same directions as the other forces so we can't use Newton's second law. We need to separate the gravity vector into components parallel and perpendicular to the ground.
$$F_{g}=mg$$-
$$\text{perpendicular to ground}$$
$$F_{g\perp}=F_{g}\cos(\theta)$$ $$F_{g\perp}=mg\cos(\theta)$$ -
$$\text{parallel to ground}$$
$$F_{g\parallel}=F_{g}\sin(\theta)$$ $$F_{g\parallel}=mg\sin(\theta)$$
The acceleration perpendicular to the ground is zero. This means the normal force equals the gravity component in that direction.
$$\sum F = ma$$ $$-F_k + mg \sin{\theta} = ma$$ $$-\mu_kF_N + mg \sin{\theta} = ma$$ $$-\mu_k m g \cos{\theta} + mg \sin{\theta} = ma$$ $$-\mu_k g \cos{\theta} + g \sin{\theta} = a$$ $$-\mu_k g \cos{\theta} = a - g \sin{\theta}$$ $$\mu_k g \cos{\theta} = g \sin{\theta}-a$$ $$ \boxed{\mu_k = \frac{g \sin{\theta}-a}{g \cos{\theta}}}$$The coefficient of kinetic friction is dependent on the acceleration of the body, the acceleration of gravity, and the angle of the incline.