Conservation of Energy

The law of conservation of energy states that the energy of a closed system is constant. Like momentum, energy can't be reduced or increased, but energy does change form.

k =  N/m
m = kg                
 
 

Question: What energies are being traded in the spring and mass system?
answer

elastic potential energy and kinetic energy


Question: When is the velocity the highest?
answer

The kinetic energy and velocity are highest when the spring energy is lowest, at the point of equilibrium. (The dotted line)


Question: How does the total energy change as the spring oscillates.
answer

The total energy is always the same for the same mass and spring constant.

With an actual spring system the energy would eventually change forms into thermal energy, but this simulation doesn't include heat loss.

The total energy is always the same value. This means we can build an equation that sets the total energy at one time equal to the total energy at any other time.

Energy cannot be created or destroyed, but it can change forms.

$$E_i = E_f$$

\( E_i \) = initial energy [J]
\( E_f \) = final energy [J]

$$K + U_g + U_s = K + U_g + U_s$$

\( K \) = kinetic energy [J]
\( U_g \) = gravitational potential energy [J]
\( U_s \) = elastic potential energy [J]

We've only covered 3 types of energy. As we learn more types the equation can gain new terms. We don't have to include every term in the equation. Only include types of energy that change.

  • If an object changes speed, include kinetic energy.
  • If an object moves vertically, include gravitational potential energy.
  • If a spring is compressed, include spring potential energy.

    • For now, we will assume no thermal energy loss, but we will explore it in the next section, thermodynamics.

    m v h Example: Build a conservation of energy equation for dropping a ball.
    strategy

    This equation only needs to include kinetic and gravitational potential energy. Initial kinetic energy is zero because the ball starts at rest. Choosing the final height to be zero will set the final gravitational potential energy to zero.

    solution $$U_g = K$$ $$mgh = \frac{1}{2}mv^2$$ $$\cancel{m}gh = \frac{1}{2} \cancel{m}v^2$$ $$gh = \frac{1}{2}v^2$$ $$\boxed{v^2 = 0+2gh}$$

    This energy equation happens to be the same as one of the equations of motion for constant acceleration.

    $$v^2 = u^2 + 2a\Delta x$$
    Example: A ball falls from rest off a 0.80 m table. Before we solve this problem, what final and initial energies can we set to zero?
    answer

    The velocity is at rest initially. This means that the initial kinetic energy will be zero as well.

    We can choose to make height zero at the bottom of the table. This means there is no final gravitational potential energy.


    How fast is the ball going just before it hits the ground?
    solution $$K_i + U_i = K_f + U_f$$ $$0+U_g = K+0$$ $$mgh = \tfrac{1}{2}mv^{2}$$ $$gh = \tfrac{1}{2}v^{2}$$ $$(9.8 \, \mathrm{\tfrac{m}{s^2}})(0.80\,\mathrm{m}) = \tfrac{1}{2}v^{2}$$ $$15.68\, \mathrm{\tfrac{m^2}{s^2}} = v^{2}$$ $$\pm 3.959\, \mathrm{ \tfrac{m}{s} } = v$$
    Example: If you throw a ball straight up at 10 m/s, how high will it go?
    solution $$K = U_g$$ $$\tfrac{1}{2}mv^{2} = mgh$$ $$\tfrac{1}{2}v^{2} = gh$$ $$\tfrac{1}{2}(10)^{2} = 9.8h$$ $$50 = 9.8h$$ $$5.10 \, \mathrm{m} = h$$
    Question: Which frictionless slope will give you the highest speed at the bottom? Explain your choice.
    answer

    Each path starts with the same gravitational potential energy. This energy is converted to the same kinetic energy.

    They will all have the same speed, but in different directions.

    Example: A 0.43 kg soccer ball kicked at 10 m/s rolls down a 30 m tall hill. How fast will the ball be moving at the bottom of the hill?
    solution

    Some of the energy is converted into heat through friction, and into rotational kinetic energy. We can't track those energy types so it will limit the accuracy of our answer.

    $$U_{g} + K_{i} = K_{f}$$ $$mgh + \tfrac{1}{2}mu^{2} = \tfrac{1}{2}mv^{2}$$ $$gh + \tfrac{1}{2}u^{2} = \tfrac{1}{2}v^{2}$$ $$(9.8)(30) + \frac{1}{2}(10)^{2} = \frac{1}{2}v^{2}$$ $$294 + 50 = \tfrac{1}{2}v^{2}$$ $$344 = \tfrac{1}{2}v^{2}$$ $$\pm 26.2 \mathrm{\tfrac{m}{s}} = v$$
    Example: A roller coaster cart starts at rest 328 ft high on the top of the first drop on "Superman: Escape from Krypton" at Six Flags Magic Mountain. How fast is the cart going at the bottom of the hill?
    solution $$328\,\mathrm{ft} \left(\frac{0.3048 \,\mathrm{m}}{1 \,\mathrm{ft}} \right) = 100 \,\mathrm{m}$$
    $$U_{g} = K$$ $$mgh = \tfrac{1}{2}mv^{2}$$ $$gh = \tfrac{1}{2}v^{2}$$ $$(9.8)(100) = \tfrac{1}{2}v^{2}$$ $$980 = \tfrac{1}{2}v^{2}$$ $$\pm 44.3 \, \mathrm{\tfrac{m}{s}} = v$$
    A B C D Example: A frictionless roller coaster starts from rest at point A. What is the velocity of the roller coaster at points B, C, and D. Assume each grid square is 10 m × 10 m.
    solution

    Conservation of energy for gravitational and kinetic energy is independent of mass.

    $$\text{point A}$$ $$E_A = mgh$$ $$\frac{E_A}{m} = gh$$ $$\frac{E_A}{m} = (9.8)(100)$$ $$\frac{E_A}{m} = 980 \, \mathrm{\tfrac{J}{kg}}$$

    Now we can set the energy / mass at point A equal to the energy / mass at points B,C,D.

    $$\text{point B}$$ $$E_A = E_B$$ $$980 = gh + \tfrac{1}{2}v^2$$ $$980 = (9.8)(8) + \tfrac{1}{2}v^2$$ $$980 - 78.4 = \tfrac{1}{2}v^2$$ $$1803.2 = v^2$$ $$v = 42.5 \, \mathrm{\tfrac{m}{s}}$$
    $$\text{point C}$$ $$980 = (9.8)(47) + \tfrac{1}{2}v^2$$ $$v = 32.2 \, \mathrm{\tfrac{m}{s}}$$
    $$\text{point D}$$ $$980 = (9.8)(20) + \tfrac{1}{2}v^2$$ $$v = 39.6 \, \mathrm{\tfrac{m}{s}}$$



    θ = 90° θ = 45° θ = 30° v = 0 Example: A ball on a 1.0 meter long string is let go at a 30° angle. Calculate the velocity at 45° and 90° as it swings back and forth.
    convert angles into heights $$h = (1.0)sin(30) = 0.5 \,\mathrm{m}$$ $$h = (1.0)sin(90) = 1\,\mathrm{m}$$ $$h = (1.0)sin(45) = 0.71\,\mathrm{m}$$ h = -1.00 m h = -0.71 m h = -0.5 m 45° 30°
    solution 90° $$K_i + U_i = K_f + U_f$$ $$U_{gi} = K +U_{gf}$$ $$mgh_i = \tfrac{1}{2}mv^2 + mgh_f$$ $$gh_i = \tfrac{1}{2}v^2 + gh_f$$ $$(9.8)(-0.5) = \tfrac{1}{2}v^2 + (9.8)(-1)$$ $$(9.8)(0.5) = \tfrac{1}{2}v^2$$ $$3.13 \, \tfrac{m}{s} = v $$
    solution 45° $$K_i + U_i = K_f + U_f$$ $$U_{gi} = K +U_{gf}$$ $$mgh_i = \tfrac{1}{2}mv^2 + mgh_f$$ $$gh_i = \tfrac{1}{2}v^2 + gh_f$$ $$(9.8)(-0.5) = \tfrac{1}{2}v^2 + (9.8)(-0.71)$$ $$(9.8)(0.21) = \tfrac{1}{2}v^2$$ $$2.03 \, \tfrac{m}{s} = v $$
    x = -0.15 m v = 0 x = 0 v = ? x = ? v = 0 Example: A 0.20 kg ball is placed on a spring compressed down 0.15 m. The internet says that your spring has a spring constant of 200.0 N/m.

    How fast should the ball be moving right after it leaves the spring?
    solution

    If we define h to be zero at the spring equilibrium, then h=x.

    $$U_s + U_g = K$$ $$\tfrac{1}{2}kx^{2} + mgh= \tfrac{1}{2}mv^{2}$$ $$\tfrac{1}{2}kx^{2} + mg x= \tfrac{1}{2}mv^{2}$$ $$\tfrac{1}{2}(200)(-0.15)^{2} + (0.2)(9.8)(-0.15)= \tfrac{1}{2}(0.2)v^{2}$$ $$1.956 = 0.1v^{2}$$ $$4.42 \, \mathrm{\tfrac{m}{s}} = v$$

    How high will the ball go?
    solution $$K = U_g$$ $$\tfrac{1}{2}mv^{2} = mgh$$

    We know from the previous question that the total energy is 1.956 J.

    $$1.956 = (0.20)(9.8)h$$ $$1.956 = 1.96h$$ $$1.00 \, \mathrm{m} = h$$
    dampening:   none full
    KE = ½mv² Us = ½kx² Ug = mgh 0 m play
    k =  kg/s²
    m =  kg

    Example: How fast is the mass moving at the spring equilibrium (x = 0)?
    Use the default values.
    solution

    We will define h = 0 at x = 0. This makes x = h.

    $$\tfrac{1}{2}mv^2 + mgh + \tfrac{1}{2}kx^2$$ $$\tfrac{1}{2}mv^2 + mgx + \tfrac{1}{2}kx^2$$

    The initial energy will be when the spring and height are at equilibrium (x = 0). The final energy will be at the lowest point, when the spring is at rest (v = 0).

    $$v_i = \, ? \quad x_i =0 \quad \quad \quad \quad v_f = 0 \quad x_f = -150$$ $$\tfrac{1}{2}mv^2 + mgx + \tfrac{1}{2}kx^2 = \tfrac{1}{2}mv^2 + mgx + \tfrac{1}{2}kx^2$$ $$\tfrac{1}{2}mv^2 = mgx + \tfrac{1}{2}kx^2$$ $$\tfrac{1}{2}(13)v^2 = (13)(9.8)(-150) + \tfrac{1}{2}(10)(-150)^2$$ $$6.5v^2 = -19110 + 112500$$ $$6.5v^2 = 93390$$ $$v = \pm 119.9 \tfrac{m}{s}$$

    Example: When the dampening is turned on, the spring system slowly settles on a single position. Write an equation to predict that position in terms of the mass and spring constant.
    strategy

    To build the equation, solve Newton's second law for an acceleration of zero.

    solution
    $$\sum F = ma $$ $$F_s-F_g = ma $$ $$-kx-mg = 0 $$ $$-kx = mg $$ $$\boxed{x = -\frac{mg}{k} }$$
    m m F s F g

    Is this equation correct? Test it out with the simulation.

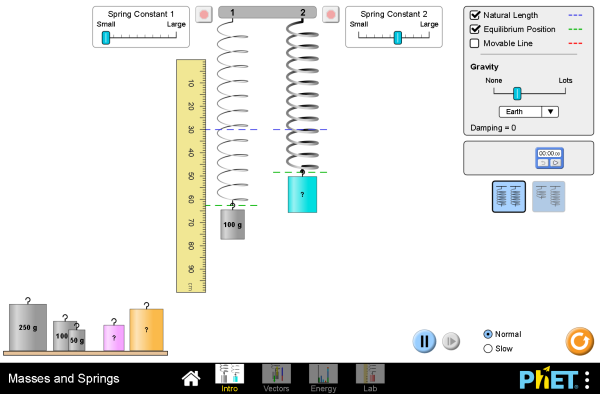
    Masses and Springs
    Click to Run
    Open the PhET simulation, switch to the energy lab mode on the bottom right.

    Investigation: What is the value of the spring constant?
    Use Newton's second law to find the solution.
    solution

    We need to solve a Newton's second law equation. Add a known mass to the hook and click stop to get the velocity and acceleration to zero.

    $$\sum F = ma$$ $$F_s-F_g = ma$$ $$kx-mg = 0$$ $$kx=mg$$ $$k=\frac{mg}{x}$$

    We can read mass and gravity directly from the simulation. We can measure the displacement with the ruler. This is easier if you check the displacement box in the top right.

    $$m=0.100 \,\mathrm{kg} \quad g=9.8\,\mathrm{\tfrac{m}{s^2}} \quad x=0.17\,\mathrm{m} $$ $$k=\frac{(0.100)(9.8)}{0.17}$$ $$k=5.8 \, \mathrm{\tfrac{kg}{s^2}}$$


    Investigation: What is the value of the spring constant?
    Use conservation of energy to find the solution.
    solution

    Conservation of energy requires two different moments in time. This simulation makes velocity impossible to measure, so we must choose two moments where v = 0.

    Point one will be at spring equilibrium. Place the 100 g mass on the hook and let it get exactly at the point of spring equilibrium. This is easier if you check the displacement box in the top right.

    Point two will be at the bottom of the springs drop. Make sure dampening is off so we don't lose energy to heat.

    $$K_i + U_{gi} + U_{si} = K_f + U_{gf} + U_{sf}$$

    The velocity is zero at both moments. If we define height to be zero at the spring equilibrium, then both potential energies are zero at the start.

    $$0 = U_g + U_s$$ $$0 = mgx + \tfrac{1}{2}kx^2$$ $$0 = mg + \tfrac{1}{2}kx$$ $$-\tfrac{1}{2}kx = mg$$ $$k=\frac{-2mg}{x}$$

    We can read mass and gravity directly from the simulation. We can measure the displacement with the ruler. This is easier if you check the displacement box in the top right. Also slow motion and pause help.

    $$m=0.100 \,\mathrm{kg} \quad g=9.8\,\mathrm{\tfrac{m}{s^2}} \quad x=-0.34\,\mathrm{m} $$ $$k=\frac{-2(0.100)(9.8)}{-0.34}$$ $$k=5.8 \, \mathrm{\tfrac{kg}{s^2}}$$


    Investigation: Calculate the mass of the red and blue weights.
    solution

    We can just reuse our method for getting the spring constant, but for mass.

    $$k=\frac{mg}{x}$$ $$m=\frac{kx}{g}$$

    Place each mass on the hook with dampening on high, and measure how much it displaces the spring.

    $$\text{blue mass}$$ $$m=\frac{(5.8)(0.38)}{(9.8)}$$ $$m=0.224\, \mathrm{kg}$$
    $$\text{red mass}$$ $$m=\frac{(5.8)(0.61)}{(9.8)}$$ $$m=0.361\, \mathrm{kg}$$

    Perfectly Elastic Collisions

    When objects collide the total momentum is conserved. Normally some of the kinetic energy of the objects will be converted into thermal or rotational energy, but in some situations the energy stays kinetic. A collision that doesn't lose any kinetic energy is called perfectly elastic. This means that for perfectly bouncy collisions we can use two conservation equations.

    $$m_1u_1 + m_2u_1 = m_1v_1 + m_2v_2$$ $$\frac{1}{2}m_1u_1^2 + \frac{1}{2}m_2u_2^2 = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2$$

    With two equations we can solve for two unknowns. We get these equations if we substitute one equation into the other and solve for the final velocities.

    $$v_1 = \frac{m_1-m_2}{m_1+m_2}u_1 + \frac{2m_2}{m_1+m_2}u_2$$ $$v_2 = \frac{2m_1}{m_1+m_2}u_1 + \frac{m_2-m_1}{m_1+m_2}u_2$$

    These equations are only approximations at our human scale, but at the atomic scale perfectly elastic collisions aren't unusual. So you'd get very accurate results for gas or liquid atoms colliding.

    Example: A 2 kg ball moving at 2 m/s to the right collides with a 7 kg ball at rest. Approximate the final velocities of each ball assuming that no kinetic energy is lost.
    solution $$2\, \mathrm{kg \, ball}$$ $$v_1 = \frac{m_1-m_2}{m_1+m_2}u_1 + \frac{2m_2}{m_1+m_2}u_2$$ $$v_1 = \left(\frac{2-7}{2+7} \right)2 + \left(\frac{2(7)}{2+7} \right)0$$ $$v_1 = \left(\frac{2-7}{2+7} \right)2$$ $$v_1 = -1.\overline{1} \, \mathrm{\tfrac{m}{s}} $$
    $$7\, \mathrm{kg \, ball}$$ $$v_2 = \frac{2m_1}{m_1+m_2}u_1 + \frac{m_2-m_1}{m_1+m_2}u_2$$ $$v_2 = \left(\frac{2(2)}{2+7}\right)2 + \left(\frac{7-2}{2+7}\right)0$$ $$v_2 = \left(\frac{2(2)}{2+7}\right)2$$ $$v_2 = 0.\overline{8} \, \mathrm{\tfrac{m}{s}} $$

    If the 2 colliding objects have the same mass we can simplify the equations.

    $$v_1=u_2 \quad \quad v_2=u_1 $$

    After an elastic collision objects with the same mass trade velocities.

    Example: A billiards ball is typically 0.16 kg. Although the cue ball is normally a bit heavier. The 8 ball moving at 12 m/s collides with the 3 ball at rest. Approximate the final velocities of each ball assuming no kinetic energy loss.
    solution

    Not much math here. They just trade velocities.
    The 8 ball is now at rest and the 3 ball is moving at 12 m/s.

    Practice printout.pdf

    In case you wanted more practice I used AI to make some more problems. The rest of the site I made by hand, but generating endless problems seemed safe. I did find mistakes in the AI generated problems, and there are probably some I didn't find. Let me know if something could be fixed. I also added a practice problem on each page with no solution. That's intentional. Have fun!

    Assume Earth gravity and no air resistance unless the problem says otherwise.

    Example: A 2.0 kg cart rolls down a smooth classroom track and drops 1.5 m in height. The track is curved, but ignore friction. How much gravitational potential energy does it lose, and how much kinetic energy does it gain?
    solution Gravitational potential energy changes because height changes. $$\Delta U_g=mg\Delta h$$ $$\Delta U_g=(2.0)(9.8)(-1.5)$$ $$\Delta U_g=-29.4\,\mathrm{J}$$

    The cart loses 29.4 J of gravitational potential energy.

    $$\Delta K=29.4\,\mathrm{J}$$

    If no energy is lost, that same amount becomes kinetic energy.

    Example: A spring launcher releases a cart. The spring energy decreases by 18 J while the cart stays at the same height. How much does the cart's kinetic energy change?
    solution The cart stays at the same height, so gravitational potential energy does not change. $$\Delta U_s=-18\,\mathrm{J}$$ $$\Delta U_g=0\,\mathrm{J}$$ $$\Delta K+\Delta U_s+\Delta U_g=0$$ $$\Delta K+(-18)+0=0$$ $$\Delta K=18\,\mathrm{J}$$

    The cart gains 18 J of kinetic energy.

    Example: A 0.50 kg ball is dropped from rest from a 3.0 m shelf in a storage room. Ignoring air resistance, what speed does it have just before it reaches the floor?
    solution Choose the floor as zero height. The mass cancels out, so the ball's mass does not affect the speed. $$E_i=E_f$$ $$U_{gi}=K_f$$ $$mgh=\tfrac{1}{2}mv^2$$ $$v=\sqrt{2gh}$$ $$v=\sqrt{2(9.8)(3.0)}$$ $$v=7.67\,\mathrm{m/s}$$
    Example: A 2.0 kg cart starts from rest at the top of a 1.2 m frictionless ramp. What speed does it have at the bottom?
    solution The cart starts with gravitational potential energy and ends with kinetic energy. $$E_i=E_f$$ $$U_{gi}=K_f$$ $$mgh=\tfrac{1}{2}mv^2$$ $$v=\sqrt{2gh}$$ $$v=\sqrt{2(9.8)(1.2)}$$ $$v=4.85\,\mathrm{m/s}$$
    Example: A skateboarder moves at 6.0 m/s at the bottom of a smooth hill. The board has 54 mm wheels, but ignore losses. How high can the skateboarder coast before stopping?
    solution At the bottom the energy is kinetic. At the highest point the speed is zero, so the energy is gravitational potential. $$E_i=E_f$$ $$K_i=U_{gf}$$ $$\tfrac{1}{2}mv^2=mgh$$ $$h=\frac{v^2}{2g}$$ $$h=\frac{(6.0)^2}{2(9.8)}$$ $$h=1.84\,\mathrm{m}$$
    Example: A 4.0 kg cart moving at 5.0 m/s climbs a frictionless track. At a point 0.80 m higher, how much kinetic energy does the cart still have?
    solution The cart trades some kinetic energy for gravitational potential energy. $$K_i=K_f+U_{gf}$$ $$K_f=K_i-U_{gf}$$ $$K_f=\tfrac{1}{2}mv_i^2-mgh$$ $$K_f=\tfrac{1}{2}(4.0)(5.0)^2-(4.0)(9.8)(0.80)$$ $$K_f=18.6\,\mathrm{J}$$
    Example: A 1500 g toy car starts from rest at the top of a 0.90 m track. Ignoring losses, what is its speed at the bottom?
    solution First convert the mass, even though it cancels out later. $$1500\,\mathrm{g}=1.5\,\mathrm{kg}$$ $$mgh=\tfrac{1}{2}mv^2$$ $$v=\sqrt{2gh}$$ $$v=\sqrt{2(9.8)(0.90)}$$ $$v=4.20\,\mathrm{m/s}$$
    Example: A ball is thrown straight upward at 12 m/s from a student's hand. Ignoring air resistance, how high above the hand does it rise?
    solution At the top, the ball's speed is zero. $$E_i=E_f$$ $$K_i=U_{gf}$$ $$\tfrac{1}{2}mv^2=mgh$$ $$h=\frac{v^2}{2g}$$ $$h=\frac{(12)^2}{2(9.8)}$$ $$h=7.35\,\mathrm{m}$$
    Example: A cart is moving at 8.0 m/s at the bottom of a track. What is its speed after it climbs 2.0 m higher?
    solution Mass cancels because every term contains mass. $$K_i=K_f+U_{gf}$$ $$\tfrac{1}{2}mv_i^2=\tfrac{1}{2}mv_f^2+mgh$$ $$v_i^2=v_f^2+2gh$$ $$v_f=\sqrt{v_i^2-2gh}$$ $$v_f=\sqrt{(8.0)^2-2(9.8)(2.0)}$$ $$v_f=4.98\,\mathrm{m/s}$$
    Example: A 0.20 kg ball is released from rest 80 cm above the floor. Ignoring air resistance, what kinetic energy does it have just before it hits the floor?
    solution The lost gravitational potential energy becomes kinetic energy. $$80\,\mathrm{cm}=0.80\,\mathrm{m}$$ $$K_f=U_{gi}$$ $$K_f=mgh$$ $$K_f=(0.20)(9.8)(0.80)$$ $$K_f=1.57\,\mathrm{J}$$
    Example: A 200 N/m spring is compressed 0.10 m and launches a 0.50 kg cart on a level frictionless track. What speed does the cart have after leaving the spring?
    solution Spring potential energy becomes kinetic energy. $$U_{si}=K_f$$ $$\tfrac{1}{2}kx^2=\tfrac{1}{2}mv^2$$ $$v=x\sqrt{\frac{k}{m}}$$ $$v=(0.10)\sqrt{\frac{200}{0.50}}$$ $$v=2.0\,\mathrm{m/s}$$
    Example: A spring launcher stores 6.0 J of energy and launches a 0.75 kg glider on a level frictionless track. What speed does the glider have?
    solution The spring energy becomes kinetic energy. $$U_s=K$$ $$6.0=\tfrac{1}{2}mv^2$$ $$v=\sqrt{\frac{2U_s}{m}}$$ $$v=\sqrt{\frac{2(6.0)}{0.75}}$$ $$v=4.0\,\mathrm{m/s}$$
    Example: A 0.30 kg cart is launched by a spring compressed 15 cm. The spring constant is 120 N/m. What launch speed should the cart have?
    solution Convert the spring compression to meters. $$15\,\mathrm{cm}=0.15\,\mathrm{m}$$ $$\tfrac{1}{2}kx^2=\tfrac{1}{2}mv^2$$ $$v=x\sqrt{\frac{k}{m}}$$ $$v=(0.15)\sqrt{\frac{120}{0.30}}$$ $$v=3.0\,\mathrm{m/s}$$
    Example: A 2.0 kg cart starts from rest and rolls down a 5.0 m long ramp. What is its speed at the bottom?
    answer This cannot be solved from the information given. Conservation of energy needs the vertical height change, not just the length of the ramp.
    Example: A 0.60 kg cart moving at 2.0 m/s compresses a 150 N/m spring on a level frictionless track. How far does the spring compress before the cart stops?
    solution Kinetic energy becomes spring potential energy. $$K_i=U_{sf}$$ $$\tfrac{1}{2}mv^2=\tfrac{1}{2}kx^2$$ $$x=v\sqrt{\frac{m}{k}}$$ $$x=(2.0)\sqrt{\frac{0.60}{150}}$$ $$x=0.126\,\mathrm{m}$$
    Example: A spring with k = 80 N/m is compressed 0.25 m and launches a 0.50 kg cart up a frictionless ramp. If the cart leaves the spring at the bottom of the ramp, how high does it rise before stopping?
    solution Spring potential energy becomes gravitational potential energy. $$U_{si}=U_{gf}$$ $$\tfrac{1}{2}kx^2=mgh$$ $$h=\frac{kx^2}{2mg}$$ $$h=\frac{(80)(0.25)^2}{2(0.50)(9.8)}$$ $$h=0.510\,\mathrm{m}$$
    Example: A 0.25 kg ball is launched upward by a spring and leaves the spring moving at 7.0 m/s. How high above the launch point does it rise?
    solution After the ball leaves the spring, kinetic energy becomes gravitational potential energy. $$K_i=U_{gf}$$ $$\tfrac{1}{2}mv^2=mgh$$ $$h=\frac{v^2}{2g}$$ $$h=\frac{(7.0)^2}{2(9.8)}$$ $$h=2.50\,\mathrm{m}$$
    Example: A 2.0 kg cart starts at rest 5.0 m above the bottom of a frictionless track. How fast is it moving when it is still 1.5 m above the bottom?
    solution Use only the drop in height, not the total height above the bottom. $$\Delta h=5.0-1.5$$ $$\Delta h=3.5\,\mathrm{m}$$ $$mg\Delta h=\tfrac{1}{2}mv^2$$ $$v=\sqrt{2g\Delta h}$$ $$v=\sqrt{2(9.8)(3.5)}$$ $$v=8.28\,\mathrm{m/s}$$
    Example: A 70 kg skier starts from rest at the top of a 12 m hill. Ignoring friction, what speed does the skier have at the bottom, and why did the mass not matter?
    solution Both gravitational potential energy and kinetic energy contain mass, so mass cancels. $$mgh=\tfrac{1}{2}mv^2$$ $$v=\sqrt{2gh}$$ $$v=\sqrt{2(9.8)(12)}$$ $$v=15.3\,\mathrm{m/s}$$

    The mass does not matter because a heavier skier has more starting energy but also needs more energy for the same speed.

    Example: A 0.40 kg ball moving at 3.0 m/s is 1.2 m above the floor. If it later reaches the floor with no energy lost, what is its speed there?
    solution The ball starts with both kinetic and gravitational potential energy. $$K_i+U_{gi}=K_f$$ $$\tfrac{1}{2}mv_i^2+mgh=\tfrac{1}{2}mv_f^2$$ $$v_f=\sqrt{v_i^2+2gh}$$ $$v_f=\sqrt{(3.0)^2+2(9.8)(1.2)}$$ $$v_f=5.71\,\mathrm{m/s}$$
    Example: A cart moves at 7.0 m/s at the bottom of a frictionless track. It reaches the top of a hill moving at 3.0 m/s. How high is the hill?
    solution Some of the cart's kinetic energy becomes gravitational potential energy. $$K_i=K_f+U_g$$ $$\tfrac{1}{2}mv_i^2=\tfrac{1}{2}mv_f^2+mgh$$ $$h=\frac{v_i^2-v_f^2}{2g}$$ $$h=\frac{(7.0)^2-(3.0)^2}{2(9.8)}$$ $$h=2.04\,\mathrm{m}$$
    Example: A 0.50 kg glider moving at 2.0 m/s reaches a compressed spring and stops after compressing it 0.20 m. What is the spring constant?
    solution Kinetic energy becomes spring potential energy. $$K_i=U_{sf}$$ $$\tfrac{1}{2}mv^2=\tfrac{1}{2}kx^2$$ $$k=\frac{mv^2}{x^2}$$ $$k=\frac{(0.50)(2.0)^2}{(0.20)^2}$$ $$k=50\,\mathrm{N/m}$$
    Example: A 1.2 kg ball is thrown straight upward at 5.0 m/s. A motion sensor shows the ball stops rising after 0.51 s. Use motion from earlier in the course to find the height, then check the result with energy.
    solution At the top, vertical speed has gone to zero. Use vertical motion to find the height. $$\Delta y=u\Delta t+\tfrac{1}{2}a\Delta t^2$$ $$\Delta y=(5.0)(0.51)+\tfrac{1}{2}(-9.8)(0.51)^2$$ $$\Delta y=1.28\,\mathrm{m}$$ Now compare with energy. $$h=\frac{v^2}{2g}$$ $$h=\frac{(5.0)^2}{2(9.8)}$$ $$h=1.28\,\mathrm{m}$$
    Example: A 900 kg car is moving at 18 km/h on a level road. If all of its kinetic energy could be stored in a spring with k = 20 000 N/m, how far would the spring compress?
    solution Convert the speed first. $$18\,\mathrm{km/h}=5.0\,\mathrm{m/s}$$ $$K_i=U_{sf}$$ $$\tfrac{1}{2}mv^2=\tfrac{1}{2}kx^2$$ $$x=v\sqrt{\frac{m}{k}}$$ $$x=(5.0)\sqrt{\frac{900}{20\,000}}$$ $$x=1.06\,\mathrm{m}$$
    Example: A 0.20 kg cart starts at rest on a spring compressed 10 cm. The spring constant is 180 N/m. The cart leaves the spring and climbs a frictionless track. What speed does it have after rising 0.50 m?
    solution The spring energy becomes both kinetic energy and gravitational potential energy. $$10\,\mathrm{cm}=0.10\,\mathrm{m}$$ $$U_{si}=K_f+U_{gf}$$ $$\tfrac{1}{2}kx^2=\tfrac{1}{2}mv^2+mgh$$ $$\tfrac{1}{2}mv^2=\tfrac{1}{2}kx^2-mgh$$ $$v=\sqrt{\frac{kx^2-2mgh}{m}}$$ $$v=\sqrt{\frac{(180)(0.10)^2-2(0.20)(9.8)(0.50)}{0.20}}$$

    The expression under the square root is negative, so the cart cannot reach 0.50 m.

    Example: A 0.50 kg cart starts at rest on a spring compressed 20 cm. The spring constant is 250 N/m. The cart leaves the spring, climbs a frictionless hill, and is still moving at 3.0 m/s at the top. How high is the hill?
    solution Spring energy becomes kinetic energy and gravitational potential energy. $$20\,\mathrm{cm}=0.20\,\mathrm{m}$$ $$U_{si}=K_f+U_{gf}$$ $$\tfrac{1}{2}kx^2=\tfrac{1}{2}mv^2+mgh$$ $$mgh=\tfrac{1}{2}kx^2-\tfrac{1}{2}mv^2$$ $$h=\frac{kx^2-mv^2}{2mg}$$ $$h=\frac{(250)(0.20)^2-(0.50)(3.0)^2}{2(0.50)(9.8)}$$ $$h=0.561\,\mathrm{m}$$
    Example: A 0.30 kg block slides down from rest, drops 1.4 m in height, and then compresses a 400 N/m spring on a frictionless track. How far does the spring compress when the block first stops?
    solution At the final moment the block is stopped, so the lost gravitational potential energy is stored in the spring. $$U_{gi}=U_{sf}$$ $$mg\Delta h=\tfrac{1}{2}kx^2$$ $$x=\sqrt{\frac{2mg\Delta h}{k}}$$ $$x=\sqrt{\frac{2(0.30)(9.8)(1.4)}{400}}$$ $$x=0.143\,\mathrm{m}$$
    Example: Two carts collide elastically on a level track. A 0.40 kg cart moving right at 3.0 m/s hits a 0.40 kg cart at rest. What are their final velocities?
    solution For a perfectly elastic collision between equal masses, the moving cart transfers its velocity to the cart at rest. $$v_1=0\,\mathrm{m/s}$$ $$v_2=3.0\,\mathrm{m/s}$$

    The first cart stops, and the second cart moves right at 3.0 m/s.

    Example: Two equal-mass pucks collide elastically on frictionless ice. Puck A moves right at 4.0 m/s, and puck B moves left at 1.0 m/s before the collision. What are their velocities after the collision?
    solution For a perfectly elastic collision between equal masses, the objects trade velocities. $$v_A=-1.0\,\mathrm{m/s}$$ $$v_B=4.0\,\mathrm{m/s}$$

    Puck A moves left at 1.0 m/s, and puck B moves right at 4.0 m/s.

    Example: A 2.0 kg cart moving right at 4.0 m/s collides elastically with a 6.0 kg cart at rest on a low-friction track. After the collision, the 2.0 kg cart bounces left at 2.0 m/s. Use momentum from earlier and energy from this page to find the 6.0 kg cart's final speed, then check that kinetic energy is conserved.
    solution Use momentum first. $$m_1u_1+m_2u_2=m_1v_1+m_2v_2$$ $$(2.0)(4.0)+(6.0)(0)=(2.0)(-2.0)+(6.0)v_2$$ $$8.0=-4.0+6.0v_2$$ $$v_2=2.0\,\mathrm{m/s}$$ Now check kinetic energy. $$K_i=\tfrac{1}{2}(2.0)(4.0)^2$$ $$K_i=16\,\mathrm{J}$$ $$K_f=\tfrac{1}{2}(2.0)(-2.0)^2+\tfrac{1}{2}(6.0)(2.0)^2$$ $$K_f=16\,\mathrm{J}$$

    Reading (6 minutes): Read Explainer: Kinetic and potential energy from Science News Explores. Then answer these questions.

    Why does doubling an object's speed make its kinetic energy four times larger rather than two times larger?
    answer

    Kinetic energy depends on speed squared. Doubling the speed multiplies the squared speed by four.


    A skateboarder rolls up a ramp and slows down. What energy change is taking place, and what happens as the skateboarder rolls back down?
    answer

    As the skateboarder rises, kinetic energy changes into gravitational potential energy. On the way down, gravitational potential energy changes back into kinetic energy.


    The article compares doubling mass with doubling speed. Which change has the larger effect on kinetic energy, and why?
    answer

    Doubling speed has the larger effect because it makes kinetic energy four times larger. Doubling mass only doubles kinetic energy.