The law of conservation of energy states that the energy of a closed system is constant. Like momentum, energy can't be reduced or increased, but energy does change form.
m =
Question: What energies are being traded in the spring and mass system?
answer
elastic potential energy and kinetic energy
Question: When is the velocity the highest?
answer
The kinetic energy and velocity are highest when the spring energy is lowest, at the point of equilibrium. (The dotted line)
Question: How does the total energy change as the spring oscillates.
answer
The total energy is always the same for the same mass and spring constant.
With an actual spring system the energy would eventually change forms into thermal energy, but this simulation doesn't include heat loss.
The total energy is always the same value. This means we can build an equation that sets the total energy at one time equal to the total energy at any other time.
$$E_i = E_f$$ $$K + U_g + U_s = K + U_g + U_s$$
\( K \) = kinetic energy [J]\( U_g \) = gravitational potential energy [J]
\( U_s \) = elastic potential energy [J]
We've only covered 3 types of energy. As we learn more types the equation can gain new terms. We don't have to include every term in the equation. Only include types of energy that change.
For now, we will assume no thermal energy loss, but we will explore it in the next section, thermodynamics.
strategy
This equation only needs to include kinetic and gravitational potential energy. Initial kinetic energy is zero because the ball starts at rest. Choosing the final height to be zero will set the final gravitational potential energy to zero.
solution
$$U_g = K$$ $$mgh = \frac{1}{2}mv^2$$ $$\cancel{m}gh = \frac{1}{2} \cancel{m}v^2$$ $$gh = \frac{1}{2}v^2$$ $$\boxed{v^2 = 0+2gh}$$This energy equation happens to be the same as one of the equations of motion for constant acceleration.
$$v^2 = u^2 + 2a\Delta x$$answer
The velocity is at rest initially. This means that the initial kinetic energy will be zero as well.
We can choose to make height zero at the bottom of the table. This means there is no final gravitational potential energy.
How fast is the ball going just before it hits the ground?
solution
$$K_i + U_i = K_f + U_f$$ $$0+U_g = K+0$$ $$mgh = \tfrac{1}{2}mv^{2}$$ $$gh = \tfrac{1}{2}v^{2}$$ $$(9.8 \, \mathrm{\tfrac{m}{s^2}})(0.80\,\mathrm{m}) = \tfrac{1}{2}v^{2}$$ $$15.68\, \mathrm{\tfrac{m^2}{s^2}} = v^{2}$$ $$\pm 3.959\, \mathrm{ \tfrac{m}{s} } = v$$solution
$$K = U_g$$ $$\tfrac{1}{2}mv^{2} = mgh$$ $$\tfrac{1}{2}v^{2} = gh$$ $$\tfrac{1}{2}(10)^{2} = 9.8h$$ $$50 = 9.8h$$ $$5.10 \, \mathrm{m} = h$$answer
Each path starts with the same gravitational potential energy. This energy is converted to the same kinetic energy.
They will all have the same speed, but in different directions.
solution
Some of the energy is converted into heat through friction, and into rotational kinetic energy. We can't track those energy types so it will limit the accuracy of our answer.
$$U_{g} + K_{i} = K_{f}$$ $$mgh + \tfrac{1}{2}mu^{2} = \tfrac{1}{2}mv^{2}$$ $$gh + \tfrac{1}{2}u^{2} = \tfrac{1}{2}v^{2}$$ $$(9.8)(30) + \frac{1}{2}(10)^{2} = \frac{1}{2}v^{2}$$ $$294 + 50 = \tfrac{1}{2}v^{2}$$ $$344 = \tfrac{1}{2}v^{2}$$ $$\pm 26.2 \mathrm{\tfrac{m}{s}} = v$$solution
$$328\,\mathrm{ft} \left(\frac{0.3048 \,\mathrm{m}}{1 \,\mathrm{ft}} \right) = 100 \,\mathrm{m}$$$$U_{g} = K$$ $$mgh = \tfrac{1}{2}mv^{2}$$ $$gh = \tfrac{1}{2}v^{2}$$ $$(9.8)(100) = \tfrac{1}{2}v^{2}$$ $$980 = \tfrac{1}{2}v^{2}$$ $$\pm 44.3 \, \mathrm{\tfrac{m}{s}} = v$$
solution
Conservation of energy for gravitational and kinetic energy is independent of mass.
$$\text{point A}$$ $$E_A = mgh$$ $$\frac{E_A}{m} = gh$$ $$\frac{E_A}{m} = (9.8)(100)$$ $$\frac{E_A}{m} = 980 \, \mathrm{\tfrac{J}{kg}}$$Now we can set the energy / mass at point A equal to the energy / mass at points B,C,D.
$$\text{point B}$$ $$E_A = E_B$$ $$980 = gh + \tfrac{1}{2}v^2$$ $$980 = (9.8)(8) + \tfrac{1}{2}v^2$$ $$980 - 78.4 = \tfrac{1}{2}v^2$$ $$1803.2 = v^2$$ $$v = 42.5 \, \mathrm{\tfrac{m}{s}}$$Example: A ball on a 1.0 meter long string is let go at a 30° angle. Calculate the velocity at 45° and 90° as it swings back and forth.
convert angles into heights
$$h = (1.0)sin(30) = 0.5 \,\mathrm{m}$$ $$h = (1.0)sin(90) = 1\,\mathrm{m}$$ $$h = (1.0)sin(45) = 0.71\,\mathrm{m}$$solution 90°
$$K_i + U_i = K_f + U_f$$ $$U_{gi} = K +U_{gf}$$ $$mgh_i = \tfrac{1}{2}mv^2 + mgh_f$$ $$gh_i = \tfrac{1}{2}v^2 + gh_f$$ $$(9.8)(-0.5) = \tfrac{1}{2}v^2 + (9.8)(-1)$$ $$(9.8)(0.5) = \tfrac{1}{2}v^2$$ $$3.13 \, \tfrac{m}{s} = v $$solution 45°
$$K_i + U_i = K_f + U_f$$ $$U_{gi} = K +U_{gf}$$ $$mgh_i = \tfrac{1}{2}mv^2 + mgh_f$$ $$gh_i = \tfrac{1}{2}v^2 + gh_f$$ $$(9.8)(-0.5) = \tfrac{1}{2}v^2 + (9.8)(-0.71)$$ $$(9.8)(0.21) = \tfrac{1}{2}v^2$$ $$2.03 \, \tfrac{m}{s} = v $$How fast should the ball be moving right after it leaves the spring?
solution
If we define h to be zero at the spring equilibrium, then h=x.
$$U_s + U_g = K$$ $$\tfrac{1}{2}kx^{2} + mgh= \tfrac{1}{2}mv^{2}$$ $$\tfrac{1}{2}kx^{2} + mg x= \tfrac{1}{2}mv^{2}$$ $$\tfrac{1}{2}(200)(-0.15)^{2} + (0.2)(9.8)(-0.15)= \tfrac{1}{2}(0.2)v^{2}$$ $$1.956 = 0.1v^{2}$$ $$4.42 \, \mathrm{\tfrac{m}{s}} = v$$How high will the ball go?
solution
$$K = U_g$$ $$\tfrac{1}{2}mv^{2} = mgh$$We know from the previous question that the total energy is 1.956 J.
$$1.956 = (0.20)(9.8)h$$ $$1.956 = 1.96h$$ $$1.00 \, \mathrm{m} = h$$m = kg
Example: How fast is the mass moving at the spring equilibrium (x = 0)?
Use the default values.
solution
We will define h = 0 at x = 0. This makes x = h.
$$\tfrac{1}{2}mv^2 + mgh + \tfrac{1}{2}kx^2$$ $$\tfrac{1}{2}mv^2 + mgx + \tfrac{1}{2}kx^2$$The initial energy will be when the spring and height are at equilibrium (x = 0). The final energy will be at the lowest point, when the spring is at rest (v = 0).
$$v_i = \, ? \quad x_i =0 \quad \quad \quad \quad v_f = 0 \quad x_f = -150$$ $$\tfrac{1}{2}mv^2 + mgx + \tfrac{1}{2}kx^2 = \tfrac{1}{2}mv^2 + mgx + \tfrac{1}{2}kx^2$$ $$\tfrac{1}{2}mv^2 = mgx + \tfrac{1}{2}kx^2$$ $$\tfrac{1}{2}(13)v^2 = (13)(9.8)(-150) + \tfrac{1}{2}(10)(-150)^2$$ $$6.5v^2 = -19110 + 112500$$ $$6.5v^2 = 93390$$ $$v = \pm 119.9 \tfrac{m}{s}$$Example: When the dampening is turned on, the spring system slowly settles on a single position. Write an equation to predict that position in terms of the mass and spring constant.
strategy
To build the equation, solve Newton's second law for an acceleration of zero.
solution
Is this equation correct? Test it out with the simulation.
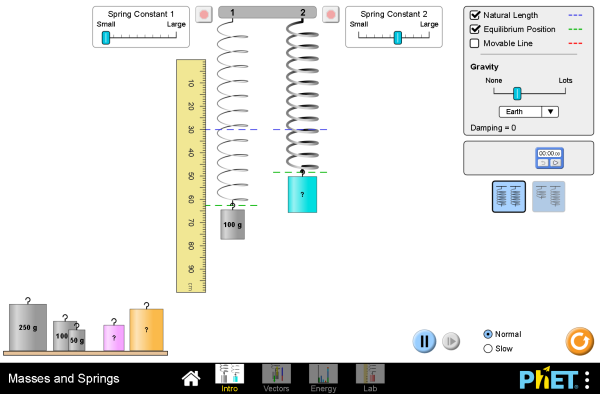
Investigation: What is the value of the spring constant?
Use Newton's second law to find the solution.
solution
We need to solve a Newton's second law equation. Add a known mass to the hook and click stop to get the velocity and acceleration to zero.
$$\sum F = ma$$ $$F_s-F_g = ma$$ $$kx-mg = 0$$ $$kx=mg$$ $$k=\frac{mg}{x}$$We can read mass and gravity directly from the simulation. We can measure the displacement with the ruler. This is easier if you check the displacement box in the top right.
$$m=0.100 \,\mathrm{kg} \quad g=9.8\,\mathrm{\tfrac{m}{s^2}} \quad x=0.17\,\mathrm{m} $$ $$k=\frac{(0.100)(9.8)}{0.17}$$ $$k=5.8 \, \mathrm{\tfrac{kg}{s^2}}$$Investigation: What is the value of the spring constant?
Use conservation of energy to find the solution.
solution
Conservation of energy requires two different moments in time. This simulation makes velocity impossible to measure, so we must choose two moments where v = 0.
Point one will be at spring equilibrium. Place the 100 g mass on the hook and let it get exactly at the point of spring equilibrium. This is easier if you check the displacement box in the top right.
Point two will be at the bottom of the springs drop. Make sure dampening is off so we don't lose energy to heat.
$$K_i + U_{gi} + U_{si} = K_f + U_{gf} + U_{sf}$$The velocity is zero at both moments. If we define height to be zero at the spring equilibrium, then both potential energies are zero at the start.
$$0 = U_g + U_s$$ $$0 = mgx + \tfrac{1}{2}kx^2$$ $$0 = mg + \tfrac{1}{2}kx$$ $$-\tfrac{1}{2}kx = mg$$ $$k=\frac{-2mg}{x}$$We can read mass and gravity directly from the simulation. We can measure the displacement with the ruler. This is easier if you check the displacement box in the top right. Also slow motion and pause help.
$$m=0.100 \,\mathrm{kg} \quad g=9.8\,\mathrm{\tfrac{m}{s^2}} \quad x=-0.34\,\mathrm{m} $$ $$k=\frac{-2(0.100)(9.8)}{-0.34}$$ $$k=5.8 \, \mathrm{\tfrac{kg}{s^2}}$$Investigation: Calculate the mass of the red and blue weights.
solution
We can just reuse our method for getting the spring constant, but for mass.
$$k=\frac{mg}{x}$$ $$m=\frac{kx}{g}$$Place each mass on the hook with dampening on high, and measure how much it displaces the spring.
Perfectly Elastic Collisions
When objects collide the total momentum is conserved. Normally some of the kinetic energy of the objects will be converted into thermal or rotational energy, but in some situations the energy stays kinetic. A collision that doesn't lose any kinetic energy is called perfectly elastic. This means that for perfectly bouncy collisions we can use two conservation equations.
$$m_1u_1 + m_2u = m_1v_1 + m_2v_2$$ $$\frac{1}{2}m_1u_1^2 + \frac{1}{2}m_2u_2^2 = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2$$With two equations we can solve for two unknowns. We get these equations if we substitute one equation into the other and solve for the final velocities.
$$v_1 = \frac{m_1-m_2}{m_1+m_2}u_1 + \frac{2m_2}{m_1+m_2}u_2$$ $$v_2 = \frac{2m_1}{m_1+m_2}u_1 + \frac{m_2-m_1}{m_1+m_2}u_2$$These equations are only approximations at our human scale, but at the atomic scale perfectly elastic collisions aren't unusual. So you'd get very accurate results for gas or liquid atoms colliding.
solution
$$2\, \mathrm{kg \, ball}$$ $$v_1 = \frac{m_1-m_2}{m_1+m_2}u_1 + \frac{2m_2}{m_1+m_2}u_2$$ $$v_1 = \left(\frac{2-7}{2+7} \right)2 + \left(\frac{2(7)}{2+7} \right)0$$ $$v_1 = 1.\overline{1} \, \mathrm{\tfrac{m}{s}} $$$$7\, \mathrm{kg \, ball}$$ $$v_2 = \frac{2m_1}{m_1+m_2}u_1 + \frac{m_2-m_1}{m_1+m_2}u_2$$ $$v_2 = \left(\frac{2(2)}{2+7}\right)2 + \left(\frac{7-2}{2+7}\right)0$$ $$v_2 = 0.\overline{8} \, \mathrm{\tfrac{m}{s}} $$
If the 2 colliding objects have the same mass we can simplify the equations.
$$v_1=u_2 \quad \quad u_1=v_2 $$After an elastic collision objects with the same mass trade velocities.
Example: A billiards ball is typically 0.16 kg. Although the cue ball is normally a bit heavier. The 8 ball moving at 12 m/s collides with the 3 ball at rest. Approximate the final velocities of each ball assuming no kinetic energy loss.solution
Not much math here. They just trade velocities.
The 8 ball is now at rest and the 3 ball is moving at 12 m/s.