Magnetism

Magnetic fields are a modification to electric fields that comes from special relativity. Like electric fields, magnetic fields are produced by charged particles, but only when the charged particle is moving.

Moving charges produce magnetic fields.

B v

A moving charge produces a magnetic field, but a moving charge also experiences a force from external magnetic fields.

Magnetic fields apply a force on moving charges.

For example, a moving electron produces a magnetic field. This field applies a force on other moving electrons.

Strong magnetic forces are produced through electromagnetism and ferromagnetism. Weaker forms of magnetism also exist, like diamagnetism and paramagnetism.

Magnetic Force on a Particle

The magnetic field in the diagram is directed out of the page. This field produces a force on moving charges. The direction of the magnetic force is inverted for negative charges.

v F v F

$$ F=qvB \sin \theta $$

\(F\) = magnetic force [N, newton, kg m/s²] vector
\(q\) = charge [C, Coulomb]
\(v\) = velocity [m/s] vector
\(B\) = external magnetic field [T, tesla, kg/C/s] vector
\(\theta\) = angle between v and B

What does ⨂ and ⊙ mean?
⨂ = into the page
⊙ = out of the page

To show 3D vectors we will use these symbols for into and out of the page. I think of the cross as the feathers on the back of an arrow, and the dot as the tip of an arrow.

Magnetic fields are measured in teslas, which can have a wide range of values.

Example: A +2 C particle is moving at 10 m/s through a 5 mT field from a refrigerator magnet. The velocity and field are at a right angle to each other. What magnitude force will be applied to the particle?
solution $$ F=qvB $$ $$ F = (2)(10)(0.005) $$ $$ F = 0.1 \, \mathrm{N} $$
Example: To measure the strength of a magnetic field, electrons are fired into the field at 100 m/s. The magnetic field accelerates the electrons at 255 m/s². What is the magnitude of the magnetic field perpendicular to the particle's velocity?
solution $$ F = ma $$ $$ F = (9.1 \times 10^{-31})(255)$$ $$ F = 2.32 \times 10^{-28} \, \mathrm{N}$$
$$ F = q v B $$ $$ B = \frac{F}{qv} $$ $$ B = \frac{2.32 \times 10^{-28}}{(1.6 \times 10^{-19})(100)} $$ $$ B = 1.45 \times 10^{-11} \, \mathrm{T} $$

Direction of Magnetic Forces

The 3D nature of the magnetic force can be solved with a vector operation called a cross product. The direction of a cross product can be found with the right hand rule.

v or I B F

Using your right hand, place your thumb in the direction of the current/charge. Place your index finger in the direction of the magnetic field. The palm of your hand will face in the direction of the force.

B v Example: What direction is the magnetic force on the charged particle?
solution

Using the right hand rule place your thumb towards the top of the page and your fingers to the right.

$$\text{into the page}$$
Example: A magnetic field is pointed north. A positively charged particle in the field is moving down, towards the ground. What direction is the magnetic force on the particle?
solution

Using the right hand rule place your thumb down and your index finger north.

$$\text{east}$$
Example: What direction magnetic field would produce a downward force on a negatively charged particle moving west?
solution

A negatively charged particle will go in the opposite direction of a positively charged particle. Using the right hand rule place your thumb west east and the palm of your hand down.

$$\text{south}$$
Example: A 1.0 C charged particle is moving west at 10 m/s through a 2 T magnetic field directed east. What is the magnitude and direction of the force on the particle?
solution

Since the velocity and magnetic field are in opposite directions there is no force.

$$F=qvB \sin \theta $$ $$\sin 180 = 0$$ $$F=0$$
Example: Find the magnitude and direction of the force on a 24 μC charge moving down at 13 m/s through an 8.5 T magnetic field directed south.
solution $$ F = q v B $$ $$ F = (24 \times 10^{-6})(13)(8.5) $$ $$ F = 0.00265 \, \text{N west}$$

Cloud chambers are a simple method of detecting high energy charged particles. In order to detect the particles, the chamber is filled with a supersaturated vapor of water or alcohol. High speed particles disrupt the vapor and leave a trail.

As radiation passes through the chamber only charged particles are visible. This is because neutral particles don't disrupt the vapor. When a powerful magnetic field is applied to the cloud chamber the charged particles curve. The arc of their curve indicates charge and mass.

Magnetic Force on a Wire

Running electric current through a wire moves a huge number of charges. Each charge follows F=qvB, but we can treat them as a whole with the concept of electric current.

derivation of magnetic force on a wire

We can substitute the definition of electric current and velocity.

$$I = \frac{q}{\Delta t} \quad \quad v = \color{teal}\frac{\Delta x}{\Delta t}$$ $$q = \color{magenta}I \Delta t \quad \quad \quad \quad \quad \, \,$$
$$F=qvB$$ $$F= {\color{magenta}(I \Delta t)} {\color{teal}\left( \frac{\Delta x}{\Delta t} \right )} B$$ $$F= I \Delta x B$$

We will use l for length instead of Δx.

$$F= I l B$$

A wire in a magnetic field will experience a force when current runs through it.

I F ℓ

$$ F=IlB \sin \theta $$

\(F\) = magnetic force [N, newton, kg m/s²] vector
\(I\) = current [A, Amps]
\(l\) = length of wire in the magnetic field [m, meter] vector
\(B\) = magnetic field [T, tesla, kg/C/s] vector
\(\theta\) = angle between the magnetic field and the current

Note that current is in the opposite direction of the flow of electrons, since electrons are negative.

The magnetic force can be used to build a rail gun.

Example: A 15 cm wire has 20 mA flowing through it east to west. The wire is in a magnetic field of 10 T directed up. Describe the force on the wire.
right hand rule v or I B F
solution $$ F=IlB$$ $$ F = (0.02)(0.15)(10) $$ $$ F = 0.03 \, \text{N north}$$
B I Example: A magnetic field is pointed to the right. Electric current is flowing towards the top of the page. What direction is the magnetic force on the wire?
solution

Using the right hand rule place your thumb towards the top of the page and your fingers to the right.

$$\text{into the page}$$
Example: How long is a wire that has a force of 0.050 N caused by the 0.21 A current interacting with a 0.45 T magnetic field at a right angle?
solution $$ F=lIB $$ $$ l= \frac{F}{IB} $$ $$ l= \frac{0.050}{(0.21)(0.45)} $$ $$ l= 0.53 \, \mathrm{m} $$

Electromagnets

The electric current from a long wire forms a magnetic field in the shape of concentric circles around the wire. The field strength diminishes with distance at 1/r not 1/r². The field strength can be calculated with Ampere's law.

I
Electric current in a straight wire produces a magnetic field that wraps around the wire.

The right hand grip rule can be used to find the direction the field turns around a wire. Place your right hand's thumb in the direction of the current. Your finger will curl in the direction the field turns.

This is different from the right hand rule used to find the force on a wire in a magnetic field.

B I
? Example: Curl the fingers on your right hand with the magnetic field to determine the direction of the current.
What does ⨂ and ⊙ mean?
⨂ = into the page
⊙ = out of the page

To show 3D vectors we will use these symbols for into and out of the page. I think of the cross as the feathers on the back of an arrow, and the dot as the tip of an arrow.

solution

Your thumb should point down. The current is directed towards the bottom of the page.

I

Two wires are aligned parallel at a constant distance of 0.3 m from each other. Each wire has 2.0 A of electric current moving towards the top of the page.

I I Example: What direction is the magnetic field produced by the current in the left wire at the location of the right wire?
solution

The field produced by the left wire is into the page on the right wire.

I

Example: What about the direction of the field from the right wire on the left?
solution

The field produced by the right wire is out of the page on the left wire.

I

Example: Use each wire's magnetic field to determine the direction of the forces between the wires.
solution

Wires with current in the same direction are pulled towards each other. I I F

This effect is part of why lightning manifests in thin strands. As electric charge travels between clouds and the ground the charge is pinched together forming lightning.

A loop of current produces a magnetic field with a north and south pole, like a ferromagnet.

The magnetic field from one wire can be increased by wrapping the wire in many loops. The strength can increased again by wrapping the wire around a ferromagnetic material, like a nail.

Electromagnets are used in most devices that produce motion from electricity: DC motors, stepper motors, servos, speakers, microphones, valves, ...

They are also used in generators, MRI machines, transformers, induction heating, magnetic levitation ...

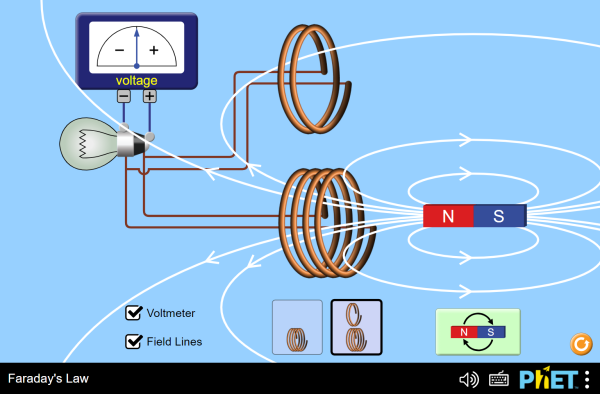
Electromagnetic induction is the production of electricity from wires moving through a magnetic field.

Induction is used to make electricity in most power generators.
Example: Nuclear, coal, hydroelectric, natural gas, and wind power

Faraday's Law
Click to Run

Ferromagnetism

Ferromagnetic metals produce a lasting magnetic field after they are exposed to an external magnetic field. Ferromagnetic metals include: iron, nickel, cobalt, most of their alloys, and rare earth metals.

Experiment: Test what materials ferromagnets are attracted to.
observations

Paper clips, staples, forks, screwdrivers, hammers, nails, scissors, refrigerators, cars, pans, speakers, microphones, batteries, phones.

Experiment: Put two ferromagnets near each other. What do you observe?
observations

One pair of ends attract and one pair repels.

A ferromagnet has a north and south pole just like an electromagnet. North and south poles attract, while two of the same poles repel.

If you break a magnet, each smaller piece also has a north and south pole. It's impossible to have a single north or south pole, a monopole.

You can see a 2D slice of the 3D field from a magnet by sprinkling small bits of iron around the magnet. The field has the same shape as the field from circular current in an electromagnet.

quantum explanation for the shape of ferromagnetic fields

Electrons do something similar to spinning around, but with some quantum mechanical differences. These electron "spins" count as moving charges, so they produce magnetic fields.

We don't see ferromagnetism in most materials because clockwise and counterclockwise electron spins cancel out. But in some materials the spins don't completely balance and we get ferromagnets.

Spinning electrons produce a magnetic field with the same shape as the field produced by electric current in a circular wire.

Magnetic field lines exit the north pole and enter the south pole. S N
Ferromagnets and electromagnets have a repulsive or attractive force that depends on which magnetic poles are facing each other.

  • Like poles repel               North+North, South+South
  • Opposite poles attract    North+South
    • derivation of the forces between north and south magnetic poles

    We learned in this example that current in parallel wires makes an attractive force and opposite current makes a repulsive force.

    Electromagnets and ferromagnets occur because they have charge moving in a circle, but it works the same way. Imagine two loops with parallel or opposite currents, and we can determine if the force between them is attractive or repulsive.

    If the current for each magnet is rotating in the same direction, the force between them is attractive. The top loop has a south pole facing down. The bottom loop has a north pole facing up.


    If the current for each magnets is rotating in opposite directions, the force between them is repulsive. Two north poles are facing each other.

    N S S N Question: What happens when you bring the north pole of a magnet close the the north pole of another magnet?
    answer

    The magnets will repel each other.

    S N S N Question: What happens when you bring the south pole of a magnet close the the north pole of another magnet?
    answer

    The magnets will attract each other.

    Question: What direction are the field lines at the north pole of a ferromagnet or an electromagnet?
    answer

    The north pole has field lines that are directed away from the magnet. The south pole as the same number of field lines directed into the magnet.

    I S N Question: What direction is the force the magnet is exerting on the wire?
    answer

    Using the right hand rule:

    the magnetic field is out of the north pole, to the right
    the electric current is up
    the force is into the page

    I S N Question: What direction is the force the magnet is exerting on the wire?
    answer

    Using the right hand rule:

    the magnetic field is out of the north pole, to the right
    the electric current is down
    the force is out of the page

    I S N Question: What direction is the force the magnet is exerting on the wire?
    answer

    This one is tricky. The field in the center of the wire is parallel with the current, so there is no force.

    The field at the left side of the magnet has a small component directed up. This produces a force on the left side of the wire directed out of the page. The field on the right side of the wire is into the page.

    These uneven forces on the sides of the wire will make it spin.

    I S N Question: What direction is the force the magnet is exerting on the wire?
    answer

    Using the right hand rule:

    the magnetic field is into the south pole, to the right
    the electric current is up
    the force is into the page

    Earth's Magnetic Field

    The Earth produces a magnetic field that is closely aligned with its axis of rotation. The source of the field is from convection of conductive materials in Earth's core, but the process is complex and has only been recently modeled with computer simulations.

    S N

    The Earth's magnetic field slows down charged particles. This shields the Earth from the solar wind's ionizing radiation. This slowing down can be seen at the north and south poles as an aurora.

    We have strong evidence that the north and south poles experience periodic reversals. About 780 000 years ago a compass would have pointed in the opposite direction it points now. The reversals are unpredictable, but typically there are thousands of years of stability between flips.

    0 10 20 30 40 50 60 70 80 90 350 340 330 320 310 300 290 280 270 180 170 160 150 140 130 120 110 100 190 200 210 220 230 240 250 260 N W E S NW SW NE SE N S

    A compass has a small magnet that aligns with the Earth's magnetic field.

    Question: The north pole of a magnet points towards the geographic north pole in the arctic circle. Does this make sense?
    answer

    This doesn't make sense. Two north poles would repel.

    The geographic north pole is actually the Earth's magnetic south pole.
    So confusing!

    Motion in a Magnetic Field

    The magnetic force on a charged particle in a uniform magnetic field is always at a 90 degree angle to the velocity. This satisfies the requirement for circular motion and it means we can set the equation for magnetic force equal to the centripetal force.

    derivation: the motion of a charged particle in a magnetic field $$ F = qvB \quad \quad F = \frac{mv^{2}}{r}$$ $$qvB = \frac{mv^{2}}{r}$$ $$qB = \frac{mv}{r}$$ $$r = \frac{mv}{qB}$$
    r v F

    $$r = \frac{mv}{qB}$$

    The Earth's magnetic field protects us from high speed charged particles. Most of these particles come from solar wind.

    Example:What is the radius for the circular motion of an electron in the Earth's magnetic field? Wikipedia says that the field is up to 70 μT, and particles from the solar wind travel at up to 500 km/s.
    solution $$r = \frac{mv}{qB}$$ $$r = \frac{(9.1 \times 10^{-31})(500\,000)}{(1.6 \times 10^{-19})(70 \times 10^{-6})}$$ $$r = 0.0406 \, \mathrm{m} $$
    Example: Find the radius for a proton in the same conditions.
    solution $$r = \frac{mv}{qB}$$ $$r = \frac{(1.67 \times 10^{-27})(500\,000)}{(1.6 \times 10^{-19})(70 \times 10^{-6})}$$ $$r = 74.55 \, \mathrm{m} $$